Задача 79779 Точки Е и F служат серединами сторон АВ...
Условие
АВСД. Доказать, что EF = (ВС + АД)/2. Вывести отсюда теорему о средней
линии трапеции.
Решение
Так как Е - середина АВ, F - середина СD, то по правилу параллелограмма сложения векторов получаем:
ОЕ^(→) =(1/2)(ОА^(→)+ОВ^(→)),
ОF^(→)=(1/2)(OD^(→)+OC^(→)).
По правилу вычитания векторов:
EF^(→)=OF^(→)-OE^(→)=(1/2)(OD^(→)+OC^(→))-(1/2)(ОА^(→)+ОВ^(→))=(1/2)(OD^(→)+OC^(→)-OA^(→)-^OB(→))=
=(1/2)((OD^(→)-OA^(→))+(OC^(→)-OB^(→)))=(1/2)(AD^(→)+BC^(→)).
Так как длина вектора равна длине отрезка, то получаем:
EF=(1/2)(AD+BC).
Что и требовалось доказать.
Если АВСD - трапеция, АD и ВС - ее основания, М и N - середины боковых сторон АВ и СD, то МN=(1/2)(AD+BC).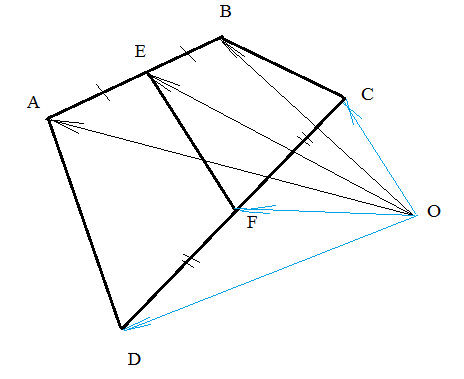
Все решения
OE = OA + 1/2 * AB
OF = OC + 1/2 * CD
2. Вектор EF:
EF = OF - OE
3. Подставим:
EF = (OC + 1/2 * CD) - (OA + 1/2 * AB) = (OC - OA) + 1/2 * (CD - AB)
4. Выразим (OC - OA) через BC и AB:
OC - OA = OB - OA + OC - OB = AB + BC
5. Подставим:
EF = (AB + BC) + 1/2 * (CD - AB) = AB + BC + 1/2 * CD - 1/2 * AB = 1/2 * AB + BC + 1/2 * CD
6. Аналогично:
AD = OD - OA = (OD - OC) + (OC - OA) = DC + (OC - OA) = -CD + (OC - OA)
7. Из шага 3:
EF = (OC - OA) + 1/2 * (CD - AB) = (AD + BC)/2
8. Следовательно:
EF = (AD + BC)/2
Теорема о средней линии трапеции:
Если ABCD — трапеция с основаниями AB || CD, а E, F — середины боковых сторон, то:
EF || AB || CD
EF = (AB + CD)/2