Задача 79768 Дан прямоугольный параллелепипед...

680a854824fa9b4da5cf2445

4/24/2025 6:48:34 PM

Дан прямоугольный параллелепипед ABCDA1B1C1D1. AA1=4, AB=8, AD=3. Точка F середина A1B1. Найдите тангенс угла между DD1 и CF. Было бы хорошо если бы показали с рисунком

626fab9a354ab65fb2f43abb

4/24/2025 7:58:41 PM

★

Смотрите рисунок.
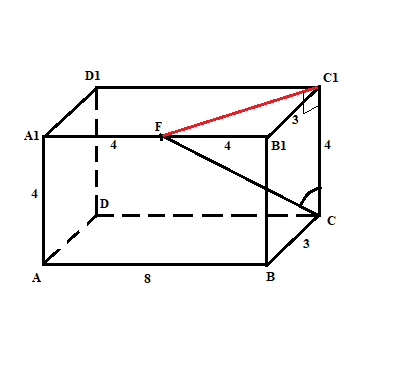
Нам нужно найти угол между прямыми DD1 и CF.
Перенесем DD1 параллельным переносом и получим CC1.
Тогда нужный нам угол - это C1CF, показанный дугой.
Построим отрезок C1F, показанный красным.
Получили прямоугольные ΔCC1F с прямым углом CC1F и ΔB1C1F с прямым углом C1B1F.
По теореме Пифагора из ΔB1C1F найдём гипотенузу C1F:
C1F = sqrt(B1C1^2 + B1F^2) = sqrt(3^2 + 4^2) = sqrt(25) = 5
В ΔCC1F tg C1CF равен отношению противолежащего катета к прилежащему:
tg C1CF = C1F/CC1 = 5/4 = 1,25

Ответ: 1,25