Задача 79743 Вычислить приближенно с помощью первого...
Условие
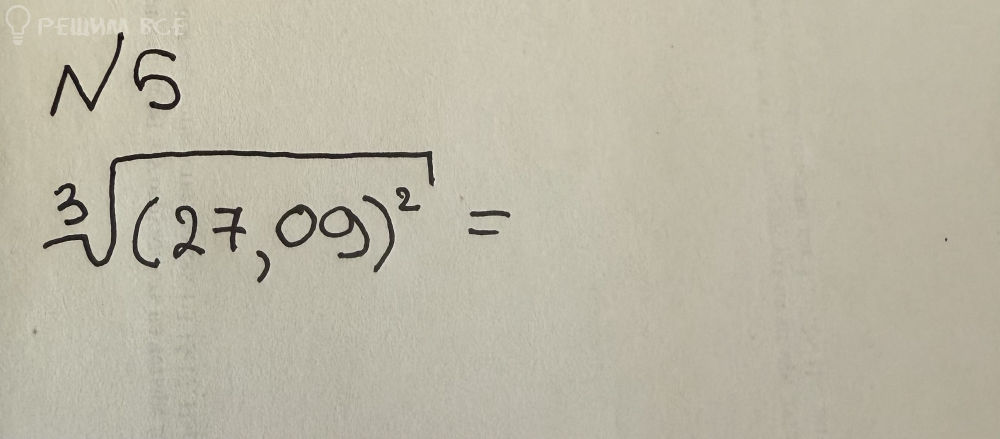
Решение
Функция: [m]\large y = x^{\frac{2}{3}}[/m]
Ее производная: [m]\large y' = \frac{2}{3} \cdot x^{\frac{2}{3} - 1} = \frac{2}{3} \cdot x^{-\frac{1}{3}} = \frac{2}{3 \sqrt[3]{x}}[/m]
Формула приближенного вычисления:
y(x) = y(x0 + Δx) = y(x0) + y'(x0)*Δx
Находим начальные значения:
x0 = 27, Δx = 0,09
[m]\large y(x0) = \sqrt[3]{27^2} = (\sqrt[3]{27})^2 = 3^2 = 9[/m]
[m]\large y'(x0) = \frac{2}{3 \sqrt[3]{27}} = \frac{2}{3 \cdot 3} = \frac{2}{9}[/m]
Вычисляем приближенное значение:
[m]\large y(x) = y(x0) + y'(x0) \cdot \Delta x = 9 + \frac{2}{9} \cdot 0,09 = 9 + 2 \cdot 0,01 = 9,02[/m]
Результат приближенного вычисления:
[m]\large \sqrt[3]{27,09^2} ≈ 9,02[/m]
Результат точного вычисления на калькуляторе:
[m]\large \sqrt[3]{27,09^2} ≈ 9,0199889[/m]
Решено верно.