Задача 79716 ...
Условие
а) 2sin²x = 1;
б) 2cos²x + cosx - 3 = 0;
в) 3tg²x + tgx - 2 = 0;
г) 2cos²x + 3sinx = 0.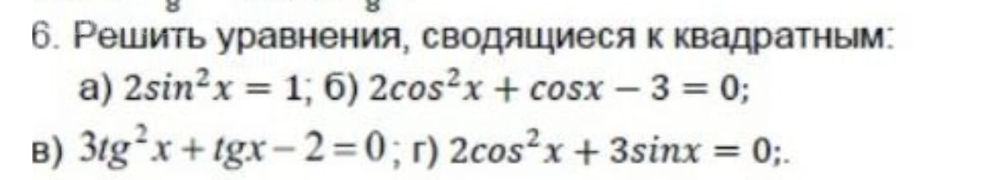
Решение
2sin^2 x - 1 = 0
(sqrt(2)*sin x + 1)(sqrt(2)*sin x - 1) = 0
sin x1 = -1/sqrt(2)
[b]x1 = (-1)^(n)*(-π/4) + π*n, n ∈ Z[/b]
sin x2 = 1/sqrt(2)
[b]x2 = (-1)^(n)*π/4 + π*n, n ∈ Z[/b]
б) 2cos^2 x + cos x - 3 = 0
Замена y = cos x; y ∈ [-1; 1]
2y^2 + y - 3 = 0
(y - 1)(2y + 3) = 0
y1 = cos x = -3/2 < -1 - решений нет
y2 = cos x = 1
[b]x = 2π*n, n ∈ Z[/b]
в) 3tg^2 x + tg x - 2 = 0
Замена y = tg x, у тангенса нет таких ограничений, как у синуса и косинуса.
3y^2 + y - 2 = 0
(y + 1)(3y - 2) = 0
y1 = tg x = -1
[b]x1 = -π/4 + π*n, n ∈ Z[/b]
y2 = tg x = 2/3
[b]x2 = arctg (2/3) + π*n, n ∈ Z[/b]
г) 2cos^2 x + 3sin x = 0
Вспоминаем, что sin^2 x + cos^2 x = 1, значит cos^2 x = 1 - sin^2 x
2 - 2sin^2 x + 3sin x = 0
Замена y = sin x, y ∈ [-1; 1]
-2y^2 + 3y + 2 = 0
Поменяем все знаки:
2y^2 - 3y - 2 = 0
D = (-3)^2 - 4*2(-2) = 9 + 16 = 25 = 5^2
y1 = sin x = (3 + 5)/4 = 8/4 = 2 > 1 - решений нет.
y2 = sin x = (3 - 5)/4 = -2/4 = -1/2
[b]x = (-1)^(n)*(-π/6) + π*n, n ∈ Z[/b]