Задача 79631 ...
Условие
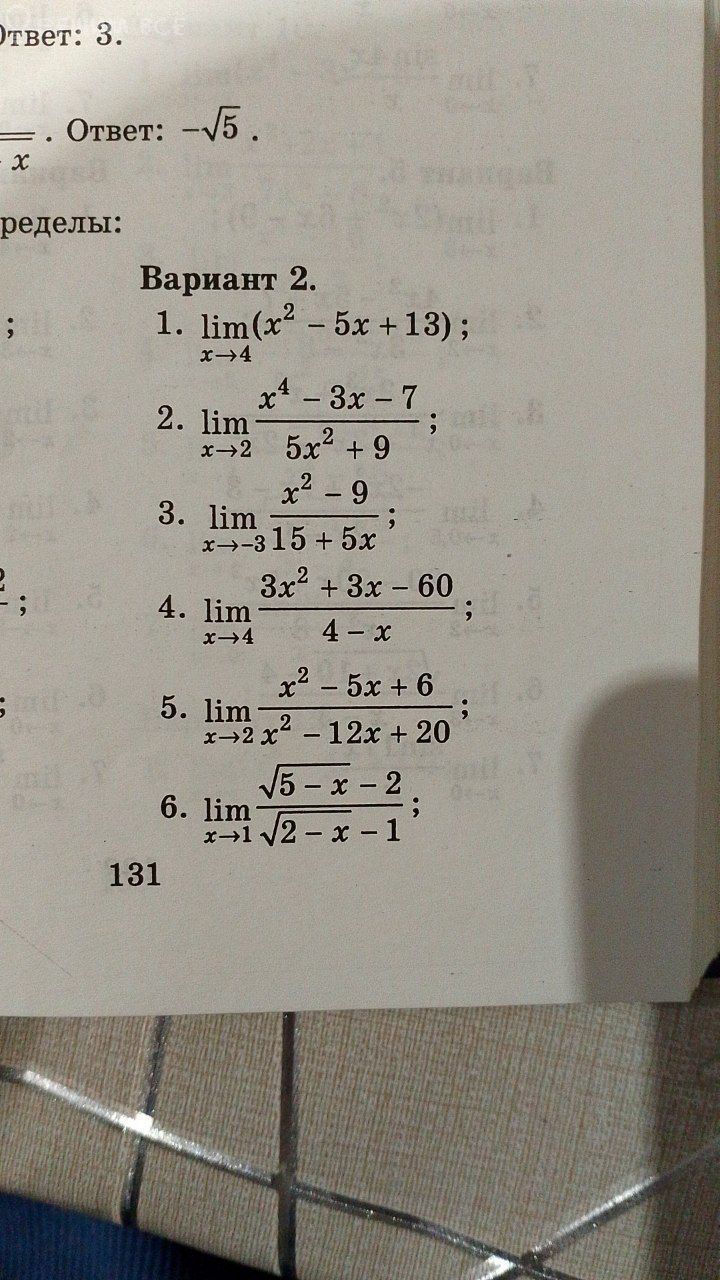
Решение
Неопределенности бывают 7 видов:
[m]\large 1) \frac{0}{0}[/m]; [m]\large 2) \frac{\infty}{\infty}[/m]; [m]\large 3) 0 \cdot \infty[/m]; [m]\large 4) \infty - \infty[/m]; [m]\large 5) 0^0[/m]; [m]\large 6) \infty^0[/m]; [m]\large 7) 1^{\infty}[/m].
Если есть неопределенность, ее нужно раскрывать сокращением, делением на x^(n),
или другими способами, например, 1 и 2 Замечательными пределами.
1) [m]\lim \limits_{x \to 4} (x^2 - 5x + 13) = 4^2 - 5 \cdot 4 + 13 = 16 - 20 + 13 = 9[/m]
Здесь достаточно подставить предел.
2) [m]\large \lim \limits_{x \to 2} \frac{x^4 - 3x - 7}{5x^2 + 9} = \frac{2^4 - 3 \cdot 2 - 7}{5 \cdot 2^2 + 9} = \frac{16 - 6 - 7}{20 + 9} = \frac{3}{29}[/m]
Здесь тоже достаточно подставить предел.
3) [m]\large \lim \limits_{x \to -3} \frac{x^2-9}{15+5x} = \frac{(-3)^2-9}{15+5(-3)} = \frac{0}{0}[/m]
Раскрываем неопределенность разложением на множители и сокращением:
[m]\large \lim \limits_{x \to -3} \frac{x^2-9}{15+5x} = \lim \limits_{x \to -3} \frac{(x-3)(x+3)}{5(3+x)} = \lim \limits_{x \to -3} \frac{x-3}{5} = \frac{-3-3}{5} =- \frac{6}{5}[/m]
4) [m]\large \lim \limits_{x \to 4} \frac{3x^2+3x-60}{4-x} = \frac{3 \cdot 4^2+3 \cdot 4 -60}{4-4} = \frac{48+12 -60}{0} = \frac{0}{0}[/m]
Раскрываем неопределенность разложением на множители и сокращением:
[m]\lim \limits_{x \to 4} \frac{3x^2+3x-60}{4-x} = - \lim \limits_{x \to 4} \frac{3(x+5)(x-4)}{x-4} = - \lim \limits_{x \to 4} \frac{3(x+5)}{1}= -3(4+5) = -3 \cdot 9 = -27[/m]
5) [m]\large \lim \limits_{x \to 2} \frac{x^2-5x+6}{x^2-12x+20} = \frac{2^2-5 \cdot 2+6}{2^2-12 \cdot 2+20} = \frac{4-10+6}{4-24+20} = \frac{0}{0}[/m]
Раскрываем неопределенность разложением на множители и сокращением:
[m]\large \lim \limits_{x \to 2} \frac{x^2-5x+6}{x^2-12x+20} = \lim \limits_{x \to 2} \frac{(x-2)(x-3)}{(x-2)(x-10)} = \lim \limits_{x \to 2} \frac{x-3}{x-10} = \frac{2-3}{2-10} = \frac{-1}{-8} = \frac{1}{8}[/m]
6) [m]\large \lim \limits_{x \to 1} \frac{\sqrt{5-x} - 2}{\sqrt{2-x} - 1} = \frac{\sqrt{5-1} - 2}{\sqrt{2-1} - 1} = \frac{\sqrt{4} - 2}{\sqrt{1} - 1}= \frac{0}{0}[/m]
Раскрываем неопределенность приведением числителя и знаменателя к разности квадратов:
[m]\large \lim \limits_{x \to 1} \frac{\sqrt{5-x} - 2}{\sqrt{2-x} - 1} = \lim \limits_{x \to 1} \frac{(\sqrt{5-x} - 2)(\sqrt{5-x} + 2)(\sqrt{2-x} + 1)}{(\sqrt{2-x} - 1)(\sqrt{2-x} + 1)(\sqrt{5-x} + 2)} = \lim \limits_{x \to 1} \frac{(5-x-2^2)(\sqrt{2-x} + 1)}{(2-x-1^2)(\sqrt{5-x} + 2)}[/m]
Теперь сокращаем:
[m]\large \lim \limits_{x \to 1} \frac{(1-x)(\sqrt{2-x} + 1)}{(1-x)(\sqrt{5-x} + 2)} = \lim \limits_{x \to 1} \frac{\sqrt{2-x} + 1}{\sqrt{5-x} + 2} = \frac{\sqrt{2-1} + 1}{\sqrt{5-1} + 2} = \frac{1 + 1}{2 + 2} =\frac{2}{4} =\frac{1}{2}[/m]