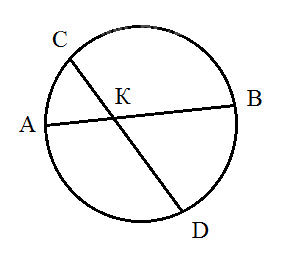
Задача 79607 В окружности проведены две хорды...

67d731878077d863e9bb9b3b

3/16/2025 8:17:37 PM

В окружности проведены две хорды пересекающиеся в точке К, КС=6, АК=8 см, ВК+ДК=28 см. Найдите длины ВК и ДК

5f3eaa23faf909182968dde0

3/17/2025 10:53:52 AM

★

Пусть DК=x, тогда BК=28-x.
По теореме об отрезках пересекающихся хорд получаем:
АК*ВК=СК*DК,
8(28-х)=6х,
14х=28*8,
х=28*8:14,
х=16.
DК=16, ВК=28-16=12.
Ответ: ВК=12, DК=16.