Задача 79589 Задание на картинке. Вычислите пределы,...
Условие
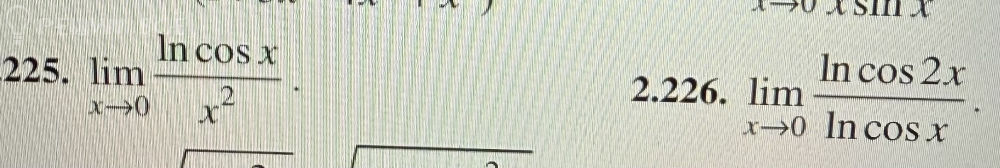
Решение
ln (1 + x) ∼ x при x → 0
1) [m]\large \lim \limits_{x \to 0} \frac{\ln \cos x}{x^2}[/m]
У нас не x, а cos x. Поэтому его надо преобразовать:
cos x = 1 - 2sin^2 (x/2)
Так как x → 0, то 2sin^2 (x/2) → 0, поэтому:
ln cos x ∼ -2sin^2 (x/2)
[m]\large \lim \limits_{x \to 0} \frac{\ln \cos x}{x^2} = \lim \limits_{x \to 0} \frac{-2 \sin^2 (x/2)}{x^2} = -2 \lim \limits_{x \to 0} \frac{\sin^2 (x/2)}{x^2} = [/m]
[m]\large = -2 \lim \limits_{x \to 0} \frac{\sin^2 (x/2)}{(x/2)^2 \cdot 2^2} = -\frac{2}{4} \lim \limits_{x \to 0} \frac{\sin^2 (x/2)}{(x/2)^2} = -\frac{2}{4} \cdot 1 = -\frac{1}{2}[/m]
Здесь я применил 1 Замечательный предел:
[m]\large \lim \limits_{t \to 0} \frac{\sin t}{t} = 1[/m]
Отсюда
[m]\large \lim \limits_{t \to 0} \frac{\sin^2 (x/2)}{(x/2)^2} = 1[/m]
Ответ: -1/2
2) [m]\large \lim \limits_{x \to 0} \frac{\ln \cos 2x}{\ln \cos x}[/m]
Здесь тоже самое.
cos 2x = 1 - 2sin^2 x, cos x = 1 - 2sin^2 (x/2)
ln cos 2x ∼ -2sin^2 x; ln cos x ∼ -2sin^2 (x/2)
[m]\large \lim \limits_{x \to 0} \frac{\ln \cos 2x}{\ln \cos x} = \lim \limits_{x \to 0} \frac{-2 \sin^2 x}{-2 \sin^2 (x/2)} = \lim \limits_{x \to 0} \frac{\sin^2 x}{\sin^2 (x/2)} = [/m]
[m]\large = \lim \limits_{x \to 0} \frac{\sin^2 x}{x^2} \cdot \frac{(x/2)^2}{\sin^2 (x/2)} \cdot \frac{x^2}{(x/2)^2} = \lim \limits_{x \to 0} 1 \cdot 1 \cdot \frac{x^2}{x^2/4} = 4[/m]
Ответ: 4