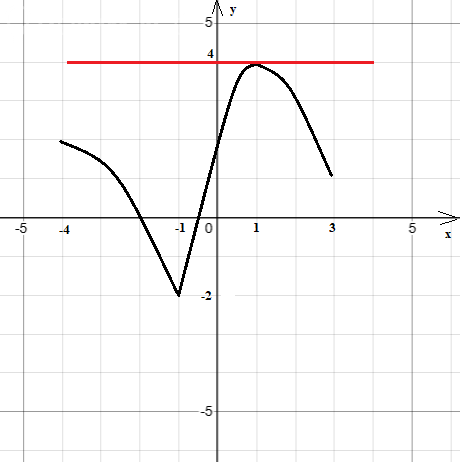
Задача 79580 № 5. Изобразите график непрерывной...
Условие
J) область определения функции есть промежуток [-4; 3];
б) значения функции составляют промежуток [-2; 4]:
н) производная функции на промежутке (-1; 1) принимает положительные
значения, а на промежутках (-4: -1) и (1: 3) - отрицательные значения;
г) график функции имеет единственную касательную, параллельную оси
абсцис.
Решение
б) Значения функции составляют [-2; 4] - это по оси Oy. На графике отметил.
в) Производная на промежутке (-1; 1) принимает положительные значения.
Значит, на этом отрезке функция возрастает.
На промежутках (-4; -1) и (1; 3) производная принимает отрицательные значения.
Значит, на этих промежутках функция убывает.
Это значит, что в точке (-2; -1) находится минимум функции.
А в точке (1; 4) находится максимум функции.
А на концах области определения в точках -4 и 3 - значения промежуточные.
г) График имеет единственную касательную, параллельную оси абсцисс.
Но при этом он имеет два экстремума - максимум и минимум.
Это значит, что в одном из экстремумов производная не существует.
Примерный график я нарисовал.
Единственная касательная, параллельная оси абсцисс, показана красным.
В точке (-1; -2) касательной нет, потому что производная не определена.
Также, как у функции y = |x| в точке x = 0.