Задача 79566 Нужно решить задачу под знак d 27...
Условие
27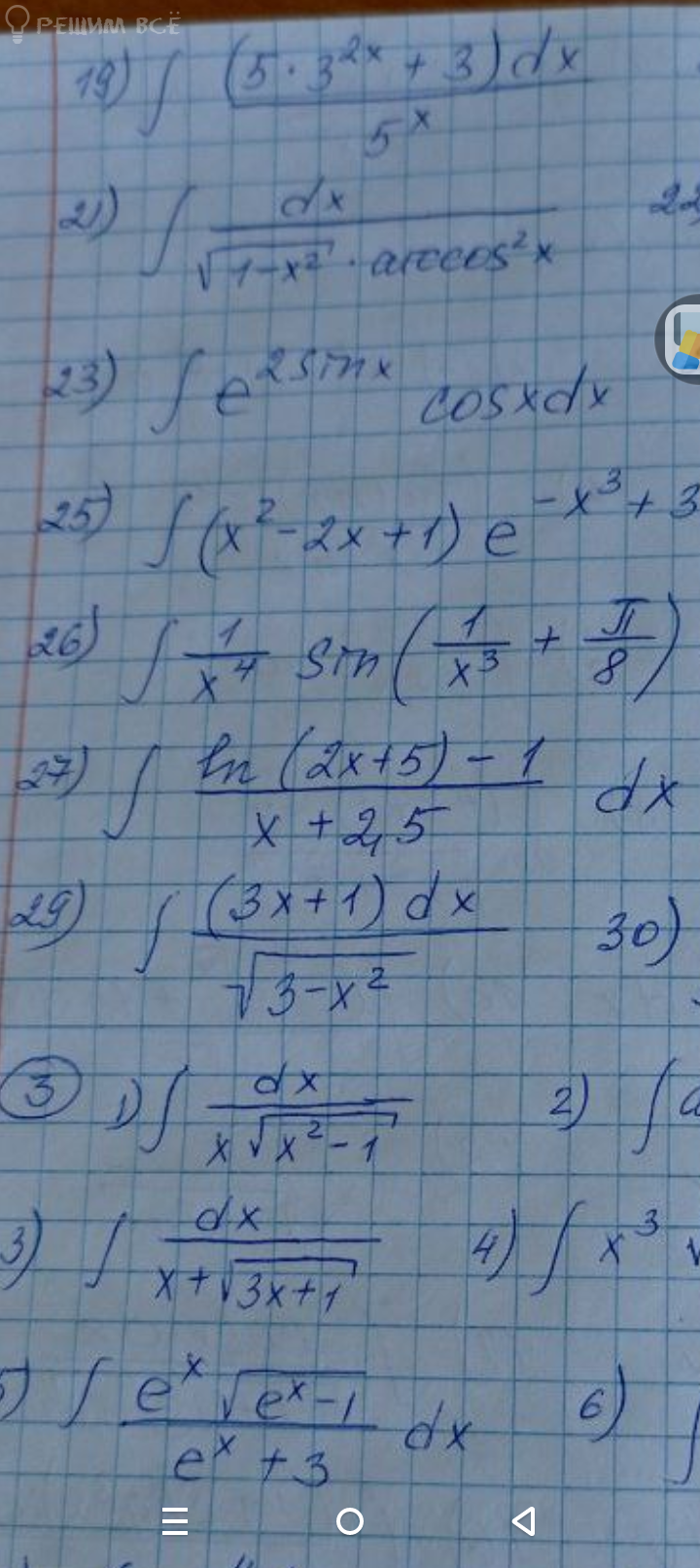
39
Решение
★
В 1 интеграле замена ln (2x + 5) = t, dt = dx/(2x + 5)
2 интеграл табличный.
[m]2 \cdot \int t\ dt - 2 \cdot \int \frac{dx}{2x + 5} = 2 \cdot \frac{t^2}{2} - 2 \cdot \frac{1}{2} \cdot \ln |2x+5| + C = [/m]
[m] = \ln^2 |2x + 5| - \ln |2x+5| + C[/m]