Задача 79554 Нужно решить уравнение (я решила, но...
Условие
3^(2x^2+7x-2) - 3^(x^2+5x) - 2*27^(x+1) = 0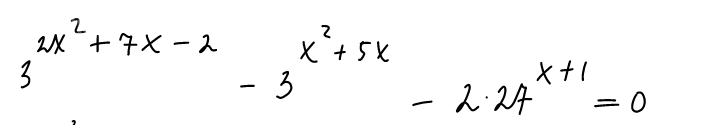
Решение
[m]3^{2x^2+10x-3x-2} - 3^{x^2 + 5x} - 2 \cdot (3^3)^{x+1} = 0[/m]
[m]3^{2(x^2+5x) - 3x-2} - 3^{x^2 + 5x} - 2 \cdot 3^{3x+3} = 0[/m]
[m]\frac{(3^{x^2+5x})^2}{3^{3x+2}} - 3^{x^2 + 5x} - 2 \cdot 3 \cdot 3^{3x+2} = 0[/m]
[m]\frac{(3^{x^2+5x})^2}{3^{3x+2}} - 3^{x^2 + 5x} - 6 \cdot 3^{3x+2}= 0[/m]
Делим всё уравнение на 3^(3x+2):
[m]\frac{(3^{x^2+5x})^2}{(3^{3x+2})^2} - \frac{3^{x^2 + 5x}}{3^{3x+2}} - 6 = 0[/m]
Замена [m]y = \frac{3^{x^2 + 5x}}{3^{3x+2}} > 0[/m] при любом x.
Получаем квадратное уравнение:
y^2 - y - 6 = 0
(y - 3)(y + 2) = 0
y = 3
[m]y = \frac{3^{x^2 + 5x}}{3^{3x+2}} = 3[/m]
[m]3^{x^2 + 5x - 3x - 2} = 3[/m]
[m]3^{x^2 + 2x - 2} = 3^1[/m]
x^2 + 2x - 2 = 1
x^2 + 2x - 3 = 0
(x + 3)(x - 1) = 0
x1 = -3; x2 = 1
Проверка:
[m]3^{2(-3)^2+7(-3)-2} - 3^{(-3)^2 + 5(-3)} - 2 \cdot 27^{-3+1} =[/m]
[m]= 3^{18-21-2} - 3^{9-15} - 2 \cdot 27^{-2} = 3^{-5} - 3^{-6} - 2 \cdot 3^{-6} =[/m]
[m]= 3^{-5} - 3 \cdot 3^{-6} = 3^{-5} - 3^{-5} = 0[/m]
Верно
[m]3^{2+7-2} - 3^{1 + 5} - 2 \cdot 27^{1+1} = 3^7 - 3^6 - 2 \cdot 3^6 = 3^7 - 3 \cdot 3^6 = 3^7 - 3^7 = 0[/m]
Верно
Ответ: x1 = -3; x2 = 1