Задача 79529 8) На рисунке изображен график функции y...
Условие
Источник: alexlarin.net, вариант 494 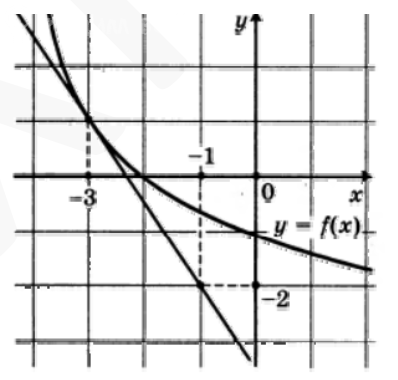
Решение
Уравнение касательной:
y = kx + b (если вы еще не учили формулу касательной через производную).
У нас касательная проходит через точки A(-3; 1); B(-1; -2)
Подставляем эти точки в уравнение, получаем систему:
{ 1 = k*(-3) + b
{ -2 = k*(-1) + b
Умножим 1 уравнение на -1:
{ 3k - b = -1
{ -k + b = -2
Складываем уравнения:
3k - b - k + b = -1 - 2
2k = -3
k = -3/2 - это и есть значение производной.
Можно и b найти.
b = -2 + k = -2 - 3/2 = -7/2