Задача 79431 Нужно исследовать фукцию полностью б...
Условие

Решение
План исследования функции.
1. Найти область определения. Выделить особые точки (точки разрыва).
D(y) = R
2. Проверить наличие вертикальных асимптот в точках разрыва и на границах области определения.
Разрывы бывают в случае ограничений:
а) Знаменатель дроби не должен равняться 0.
б) Под корнями четной степени должно быть выражение >= 0.
в) Под логарифмом должно быть выражение > 0.
Основание логарифма тоже должно быть > 0 и не равно 1.
г) Под тангенсом выражение не равно pi/2, а под котангенсом не равно 0.
В этой функции никаких ограничений нет.
Вертикальных асимптот нет.
3. Найти точки пересечения с осями координат.
Пересечение с осью Oy: x = 0
y(0) = 0^4 - 2*0^2 = 0
Точка O(0; 0)
Пересечение с осью Ox: y = 0
x^4 - 2x^2 = 0
x^2*(x^2 - 2) = 0
x1 = x2 = 0
x3 = -sqrt(2)
x4 = sqrt(2)
Точки O(0; 0); A(-sqrt(2); 0); B(sqrt(2); 0)
4. Установить, является ли функция чётной или нечётной.
y(-x) = (-x)^4 - 2(-x)^2 = x^4 - 2x^2 = y(x)
Это четная функция.
5. Определить, является ли функция периодической или нет (только для тригонометрических функций).
Функция не периодическая.
6. Найти точки экстремума и интервалы монотонности.
Точки экстремума - это точки, в которых y' = 0
y' = 4x^3 - 4x = 4x*(x^2 - 1) = 4x(x - 1)(x + 1) = 0
x1 = -1; y(-1) = (-1)^4 - 2*(-1)^2 = 1 - 2*1 = -1
Точка M(-1; -1)
x2 = 0; y(0) = 0
Точка O(0; 0)
x3 = 1; y(1) = 1^4 - 2*1^2 = 1 - 2*1 = -1
Точка N(1; -1)
Интервалы монотонности.
При x < -1 будет y' < 0, функция убывает.
При x ∈ (-1; 0) будет y' > 0, функция возрастает.
M(-1; -1) - точка минимума.
При x ∈ (0; 1) будет y' < 0, функция убывает.
O(0; 0) - точка максимума.
При x > 1 будет y' > 0, функция возрастает.
N(1; -1) - точка минимума.
7. Найти точки перегиба и интервалы выпуклости-вогнутости.
Точки перегиба - это точки, в которых y'' = 0
y'' = 12x^2 - 4 =4(3x^2 - 1) = 4(sqrt(3)*x - 1)(sqrt(3)*x + 1) = 0
x1 = -1/sqrt(3)
y(-1/sqrt(3)) = (-1/sqrt(3))^4 - 2*(-1/sqrt(3))^2 = 1/9 - 2/3 = -5/9
Точка перегиба (-1/sqrt(3); -5/9)
x2 = 1/sqrt(3)
y(1/sqrt(3)) = (1/sqrt(3))^4 - 2*(1/sqrt(3))^2 = 1/9 - 2/3 = -5/9
Точка перегиба (1/sqrt(3); -5/9)
На графике эти точки не показаны.
Интервалы выпуклости и вогнутости.
При x < -1/sqrt(3) будет y'' > 0 - график вогнутый.
При x ∈ (-1/sqrt(3); 1/sqrt(3)) будет y'' < 0 - график выпуклый.
При x > 1/sqrt(3) будет y'' > 0 - график вогнутый.
8. Найти наклонные асимптоты. Исследовать поведение на бесконечности.
Наклонные асимптоты имеют вид f(x) = k*x + b, где:
[m]k = \lim \limits_{x \to \infty} \frac{y(x)}{x} = \lim \limits_{x \to \infty} (x^3 - 2x) = +\infty[/m]
[m]b = \lim \limits_{x \to \infty} (y(x) - kx)[/m]
Так как k = +oo, то b вычислить невозможно.
Наклонных асимптот нет, при x ⇒ +-oo будет y ⇒ +oo
9. Выбрать дополнительные точки и вычислить их координаты.
M(-1; -1), N(1; -1)
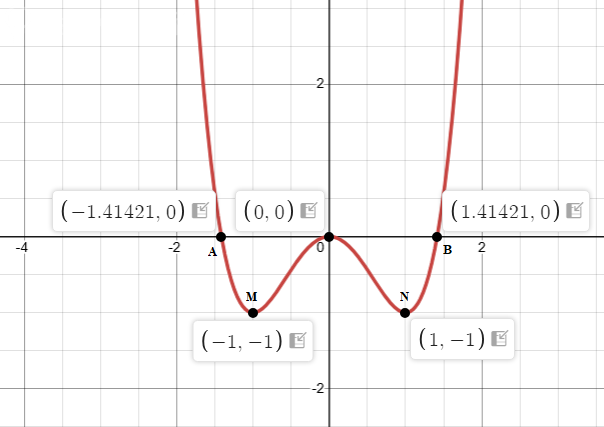
10. Построить график и асимптоты.
График прилагается.