Задача 79418 1. Три стороны описанного около...
Условие
3: 5: 4 .Найдите длину меньшей из сторон этого четырехугольника, если его периметр равен 56.
Источник: alexlarin.net, вариант 493 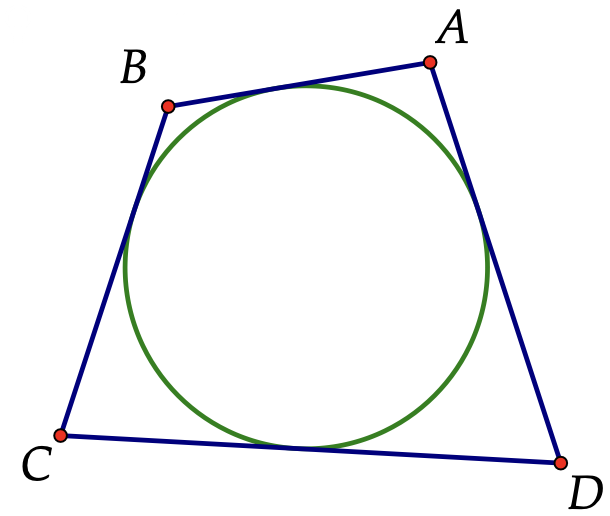
математика 10-11 класс
142
Решение
★
ВС+DA=CD+AB,
3+4=5+x,
x=2.
Значит, длина стороны АВ=2 части.
Находим периметр четырехугольника:
3+5+4+2=14 (частей).
По условию периметр равен 56 см, значит,
56:14=4 (см) - приходится на одну часть.
Наименьшая из сторон имеет длину 2 частей, значит, ее длина равна 4*2=8 (см).
Ответ: 8 см.