Задача 79389 Задание на картинке. Упростить СДНФ,...
Условие
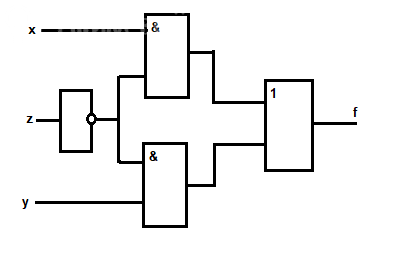
Упростить СДНФ, составить контактную схему. Также упростить СДНФ, составить логическую схему. 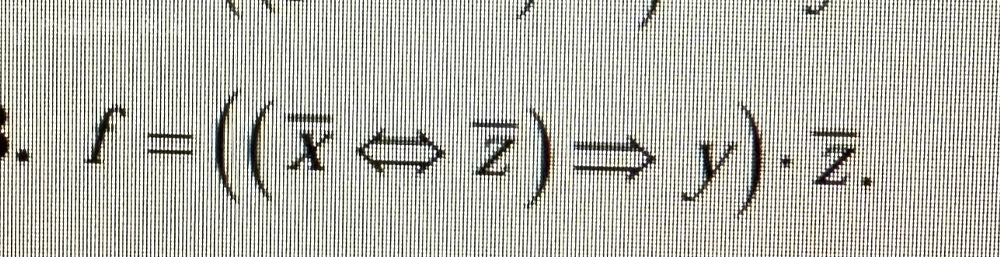
Решение
Ставить черточку над буквой я здесь не умею.
f = ((~x <=> ~z) => y) * ~z
Умножение в конце - это логическое И, обозначается /\.
Эквивалентность <=> можно раскрыть так:
A <=> B = (A /\ B) \/ (~A /\ ~B)
Импликацию => можно раскрыть так:
A => B = ~A \/ B
Подставляем:
f = [ ~((~x /\ ~z) \/ (x /\ z)) \/ y ] /\ ~z
f = [ (~(~x /\ ~z) /\ ~(x /\ z)) \/ y ] /\ ~z
f = [ ((x \/ z) /\ (~x \/ ~z)) \/ y ] /\ ~z
f = [ (x \/ z \/ y) /\ (~x \/ ~z \/ y)] /\ ~z
Так как внешние функции все одинаковые: /\, можно убрать скобки [ ].
f = (x \/ z \/ y) /\ (~x \/ ~z \/ y) /\ ~z
По закону поглощения:
(A \/ B) /\ A = A
Поэтому:
f = (x \/ z \/ y) /\ ~z = (x /\ ~z) \/ (z /\ ~z) \/ (y /\ ~z)
z /\ ~z = 0, A \/ 0 = A
Поэтому:
f = (x /\ ~z) \/ (y /\ ~z)
Это и есть СДНФ.
Таблица истинности:
x | y | z | x /\ ~z | y /\ ~z | f
0 | 0 | 0 | __ 0 __ | __ 0 __ | 0
0 | 0 | 1 | __ 0 __ | __ 0 __ | 0
0 | 1 | 0 | __ 0 __ | __ 1 __ | 1
0 | 1 | 1 | __ 0 __ | __ 0 __ | 0
1 | 0 | 0 | __ 1 __ | __ 0 __ | 1
1 | 0 | 1 | __ 0 __ | __ 0 __ | 0
1 | 1 | 0 | __ 1 __ | __ 1 __ | 1
1 | 1 | 1 | __ 0 __ | __ 0 __ | 0
Схему нарисовал, как сумел.
Чем отличается контактная от логической, я не знаю.