Задача 79304 Нужно исследовать фукцию полностью 22....

Ritta

11 февраля 2025 г. в 04:57

Нужно исследовать фукцию полностью

22. a) $y = e^{-\frac{x^2}{2}}$

Удачник66

11 февраля 2025 г. в 11:20

★

$y = e^{-\frac{x^2}{2}}$
1) Найти область определения. Выделить особые точки (точки разрыва).
Область определения: x ∈ (–oo; +oo). Точек разрыва нет.

2) Проверить наличие вертикальных асимптот в точках разрыва и на границах области определения.
Вертикальных асимптот нет

3) Найти точки пересечения с осями координат.
Пересечение с осью Oy:
y(0) = e⁰ = 1
Пересечение с осью Ox:
y = 0
$e^{-\frac{x^2}{2}} = 0$
Решений нет. Пересечений с осью Ox нет.

4) Установить, является ли функция чётной или нечётной.
Функция четная.

5) Определить, является ли функция периодической или нет (только для тригонометрических функций).
Функция не периодическая.

6) Найти точки экстремума и интервалы монотонности.
$y' = e^{-\frac{x^2}{2}} \cdot (-x) = 0$
x = 0; y(0) = 1
При x < 0 будет y' > 0 – функция возрастает.
При x > 0 будет y' < 0 – функция убывает.
x = 0 – точка максимума.

7) Найти точки перегиба и интервалы выпуклости–вогнутости.
$y'' = e^{-\frac{x^2}{2}} \cdot (-x)(-x) + e^{-\frac{x^2}{2}} \cdot (-1) = 0$
$e^{-\frac{x^2}{2}} \cdot (x^2 - 1) = e^{-\frac{x^2}{2}} (x-1)(x+1) = 0$
x1 = –1; x2 = 1 – точки перегиба.
При x < –1 будет y'' > 0 – график выпуклый вниз (вогнутый)
При x ∈ (–1; 1) будет y'' < 0 – график выпуклый вверх (выпуклый)
При x > 1 будет y'' > 0 – график выпуклый вниз (вогнутый)

8) Найти наклонные асимптоты. Исследовать поведение на бесконечности.
Наклонные асимптоты имеют вид: f(x) = k·x + b, где:
$k = \lim \limits_{x \to \infty} \frac{y(x)}{x} = \lim \limits_{x \to \infty} \frac{e^{-x^2/2}}{x} = \frac{e^{-\infty}}{\infty} = \frac{0}{\infty} = 0$
$b = \lim \limits_{x \to \infty} (y(x) - kx) = \lim \limits_{x \to \infty} (e^{-x^2/2} - 0) = e^{-\infty} = 0$
Наклонная асимптота – горизонтальная:
f(x) = 0, то есть оcь Ox.

9) Выбрать дополнительные точки и вычислить их координаты.
x = –1; $y = e^{-\frac{1}{2}} = \frac{1}{\sqrt{e}}$
x = 1; $y = e^{-\frac{1}{2}} = \frac{1}{\sqrt{e}}$

10) Построить график и асимптоты.
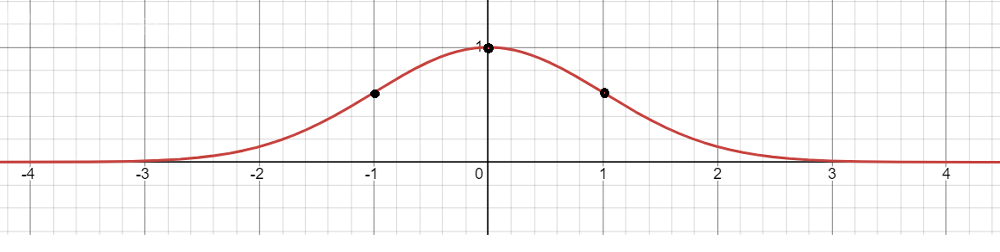
График показан на рисунке
Точка экстремума и точки перегиба тоже показаны.