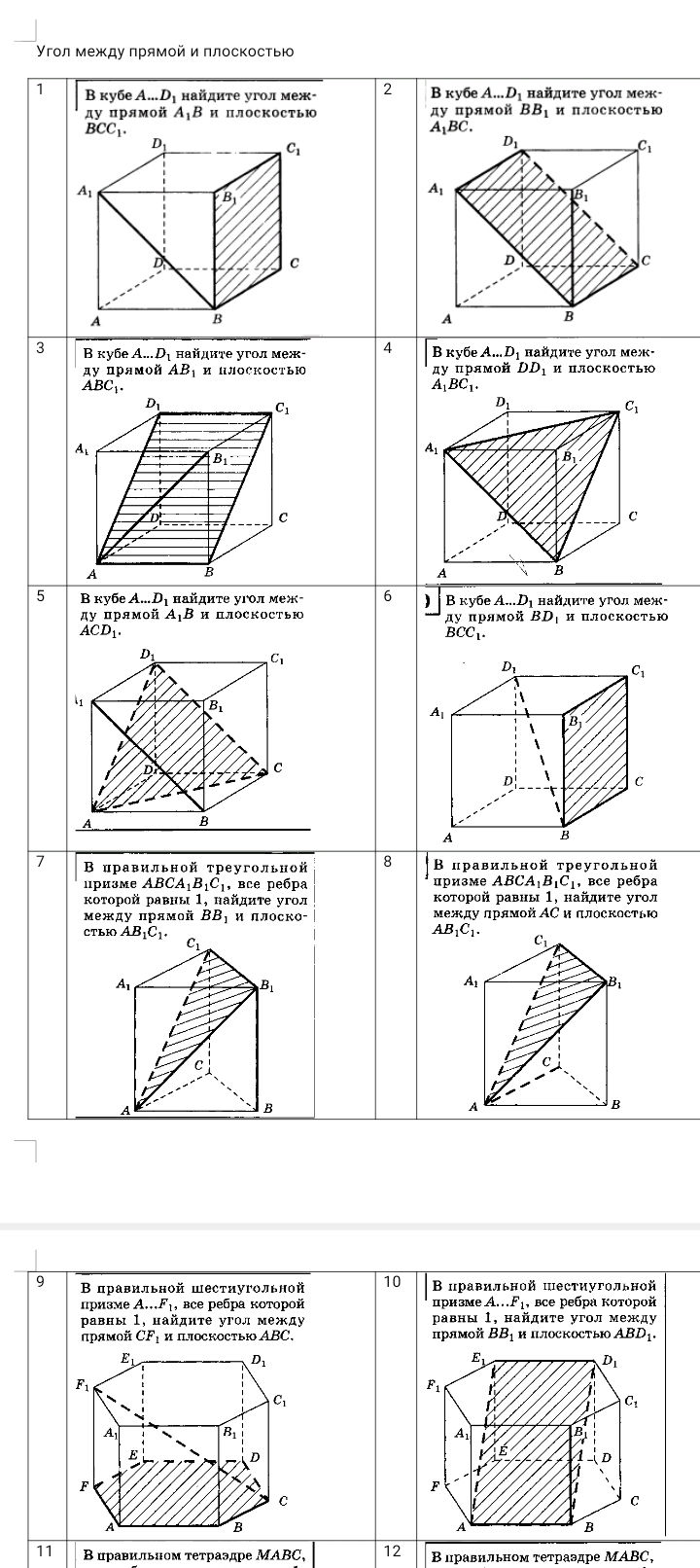
Задача 79245 5)в кубе а...д1 найдите угол между...
Условие
6)....
Решение
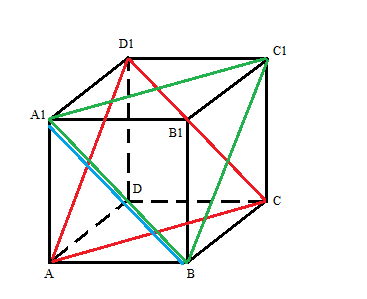
Если плоскость ACD1 (показана красным) перенести параллельным переносом, то получится плоскость BA1C1 (показана зеленым).
Тогда прямая A1B (показана синим) будет принадлежать этой плоскости.
Это значит, что прямая A1B параллельна плоскости ACD1.
Угол между ними равен 0.
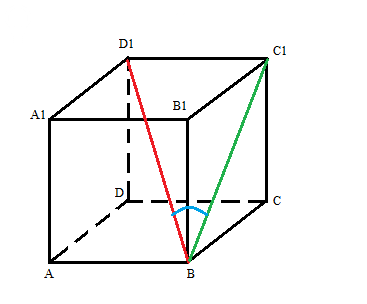
6) Смотрите рисунок 2.
Угол между прямой BD1 (показана красным) и плоскостью BCC1 - это угол между прямой BD1 и ее проекцией на плоскость BCC1.
Проекция прямой BD1 на BCC1 - это диагональ BC1 (показана зеленым).
Сам угол C1BD1 показан синим.
Рассмотрим прямоугольный треугольник BC1D1.
У него катеты C1D1 = a, BC1 = a*sqrt(2). гипотенуза BD1 = a*sqrt(3).
Мы не знаем длину ребра куба, обозначим ее а, важно, что все ребра равны.
Тогда синус угла C1BD1:
sin C1BD1 = C1D1/BD1 = a/(a*sqrt(3)) = 1/sqrt(3)
C1BD1 ≈ 35,2644° = 35° 15' 52''