Задача 79222 Нужно решить задачу , используя правило...
Условие

Решение
По правилу Лопиталя нужно взять производные от числителя и знаменателя.
[m]\lim \limits_{x \to 0} \frac{f(x)}{g(x)} = \lim \limits_{x \to 0} \frac{f'(x)}{g'(x)}[/m]
В нашем случае:
[m]\lim \limits_{x \to 0} \frac{x^2 \cos x}{\cos 3x - 1} = \lim \limits_{x \to 0} \frac{2x \cos x + x^2(-\sin x)}{-3\sin 3x} = -\lim \limits_{x \to 0} \frac{2x \cos x - x^2 \sin x}{3\sin 3x} = \frac{0+0}{0}[/m]
Получилась опять неопределённость, применим правило Лопиталя ещё раз:
[m]-\lim \limits_{x \to 0} \frac{2\cos x + 2x(-\sin x) - 2x \sin x - x^2 \cos x}{9 \cos x} = - \frac{2\cos 0 + 0 - 0 - 0}{9 \cos 0} = -\frac{2}{9}[/m]
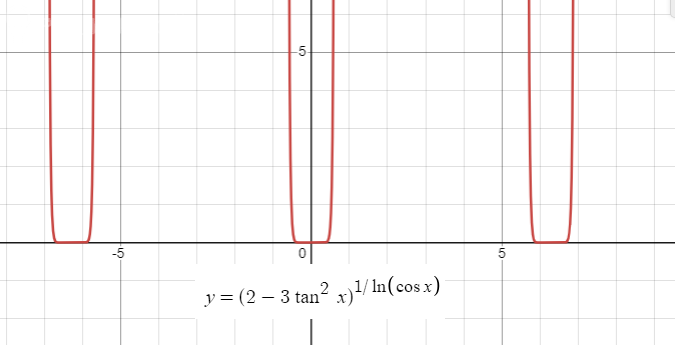
б) [m]\large \lim \limits_{x \to 0} (2 - 3 tg^2\ x)^{1/\ln \cos x}[/m]
Чтобы применить правило Лопиталя, нужно из этого получить дробь.
Применим известные свойства логарифмов:
[m]a = e^{\ln a}[/m]
[m]\ln a^{b} = b \cdot \ln a[/m]
[m]\large \lim \limits_{x \to 0} e^{\ln (2 - 3 tg^2\ x)^{1/\ln \cos x})} = \lim \limits_{x \to 0} e^{\frac{\ln (2 - 3 tg^2\ x)}{\ln \cos x}}[/m]
Теперь можно применить правило Лопиталя.
Чтобы не громоздить дроби, я вычислю числитель и знаменатель отдельно:
[m](\ln (2 - 3 tg^2\ x))' = \frac{1}{2 - 3 tg^2\ x} \cdot (-6tg\ x) \cdot \frac{1}{\cos^2 x} = -\frac{6tg\ x}{(2 - 3 tg^2\ x) \cdot \cos^2 x}[/m]
[m](\ln \cos x)' = \frac{1}{\cos x} \cdot (-\sin x) = -\frac{\sin x}{\cos x} = -tg\ x[/m]
Подставляем в наш предел:
[m]\large \lim \limits_{x \to 0} e^{-\frac{6tg\ x}{(2 - 3 tg^2\ x) \cdot \cos^2 x} : (-tg\ x)} = \lim \limits_{x \to 0} e^{\frac{6}{(2 - 3 tg^2\ x) \cdot \cos^2 x}} =[/m]
[m]= e^{\frac{6}{(2 - 0) \cdot \cos^2 0}} = e^{\frac{6}{2}} = e^{3}[/m]
Но это неправильно, по графику предел равен 0, причем с обоих сторон.
[m]\large \lim \limits_{x \to 0-0} (2 - 3 tg^2\ x)^{1/\ln \cos x} = 0[/m]
[m]\large \lim \limits_{x \to 0+0} (2 - 3 tg^2\ x)^{1/\ln \cos x} = 0[/m]
Смотрите график.