Задача 79208 Нужно решить задачу а и б...
Условие
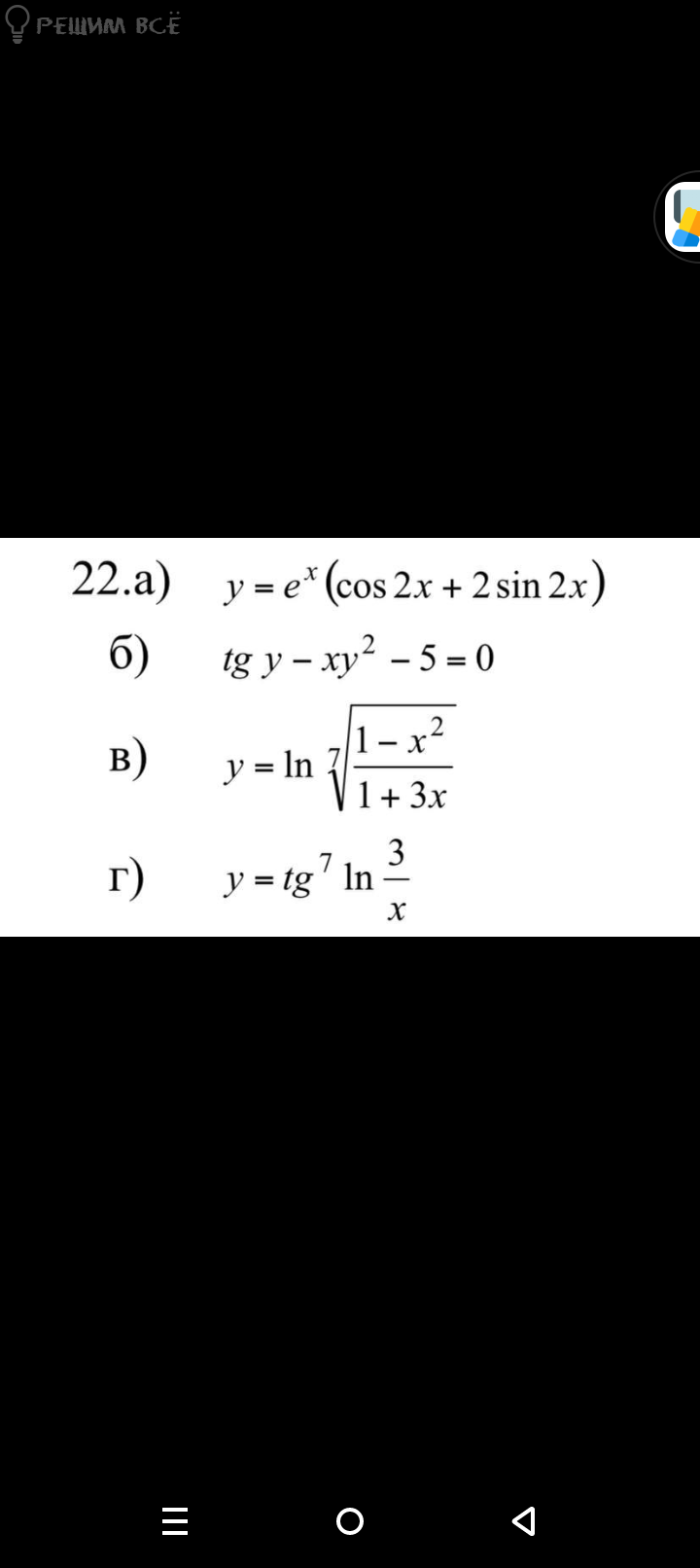
68
Решение
★
а) Произведение двух функций.
[m]y = e^{x}(\cos 2x + 2\sin 2x)[/m]
[m]y' = e^{x}(\cos 2x + 2\sin 2x) + e^{x}(-2\sin 2x + 4\cos 2x)[/m]
[m]y' = e^{x} \cdot 5\cos 2x = 5e^{x} \cdot \cos 2x[/m]
б) Неявно заданная функция.
[m]\large tg\ y - xy^2 - 5 = 0[/m]
[m]\large \frac{1}{\cos^2 y} \cdot y' - (1y^2 + x \cdot 2yy') = 0[/m]
[m]\large \frac{1}{\cos^2 y} \cdot y' - y^2 - 2xyy' = 0[/m]
[m]\large \frac{1}{\cos^2 y} \cdot y' - 2xyy' = y^2[/m]
[m]\large y' (\frac{1}{\cos^2 y} - 2xy) = y^2[/m]
[m]\large y' \cdot \frac{1 - 2xy \cos^2 y}{\cos^2 y} = y^2[/m]
[m]\large y' = \frac{y^2 \cos^2 y}{1 - 2xy \cos^2 y}[/m]