Задача 79181 Нужно решить задачу, расписать каждый...
Условие
в и г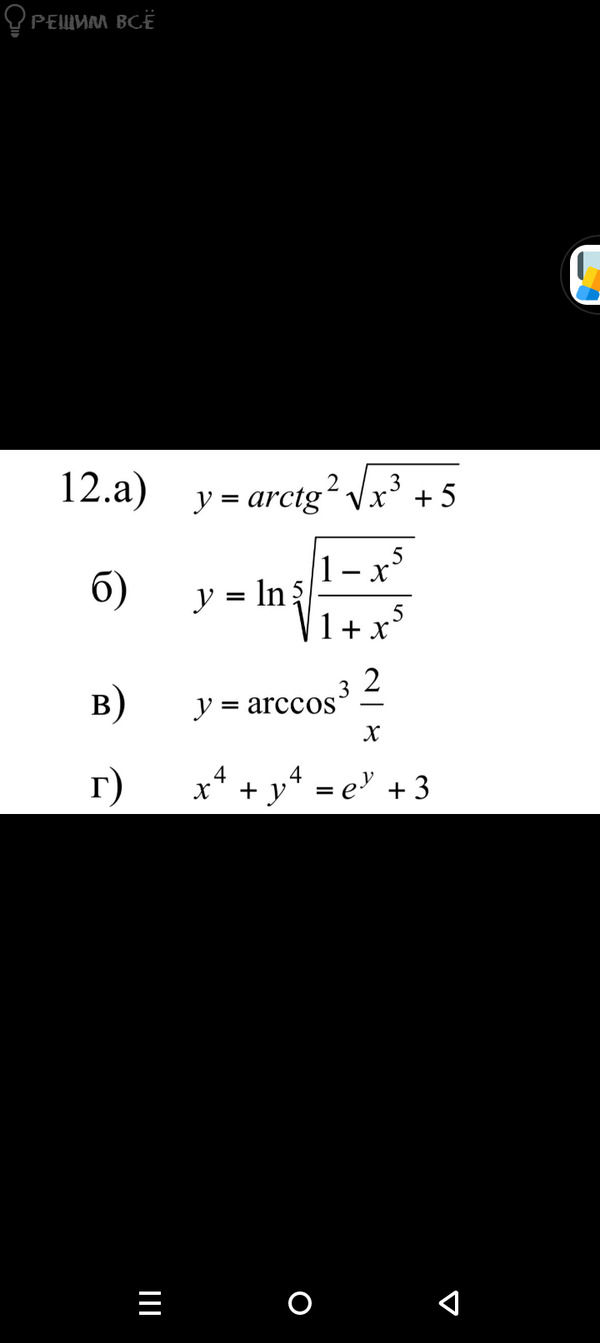
Решение
в) y = arccos^3 (2/x)
Здесь 3 функции друг в друге.
y(f) = f^3; f(g) = arccos (g); g(x) = 2/x
Берем производную от каждой функции:
[m]y'(f) = 3f^2 = 3arccos^2 \frac{2}{x}[/m]
[m]f'(g) = -\frac{1}{\sqrt{1 - g^2}} = -\frac{1}{\sqrt{1 - (2/x)^2}} = -\frac{1}{\sqrt{(x^2 - 2^2)/x^2}} = -\frac{x}{\sqrt{x^2 - 4}}[/m]
[m]g'(x) = -\frac{2}{x^2}[/m]
Перемножаем это всё:
[m]y'(x) = 3arccos^2 \frac{2}{x} \cdot (-\frac{x}{\sqrt{x^2 - 4}}) \cdot (-\frac{2}{x^2}) = 6arccos^2 \frac{2}{x} \cdot \frac{1}{x \sqrt{x^2 - 4}}[/m]
г) x^4 + y^4 = e^(y) + 3
Функция задана неявно, берем от нее дифференциал.
4x^3 + 4y^3*y'(x) = e^(y)*y'(x) + 0
Отделяем y' от всего остального:
4x^3 = e^(y)*y'(x) - 4y^3*y'(x)
Выносим y' за скобки и записываем его слева, а остальное справа:
y'(x)*(e^(y) - 4y^3) = 4x^3
Выражаем y'(x) через x и y:
[m]\large y'(x) = \frac{4x^3}{e^{y} - 4y^3}[/m]