Задача 79180 Нужно решить задачу, расписать каждый...
Условие
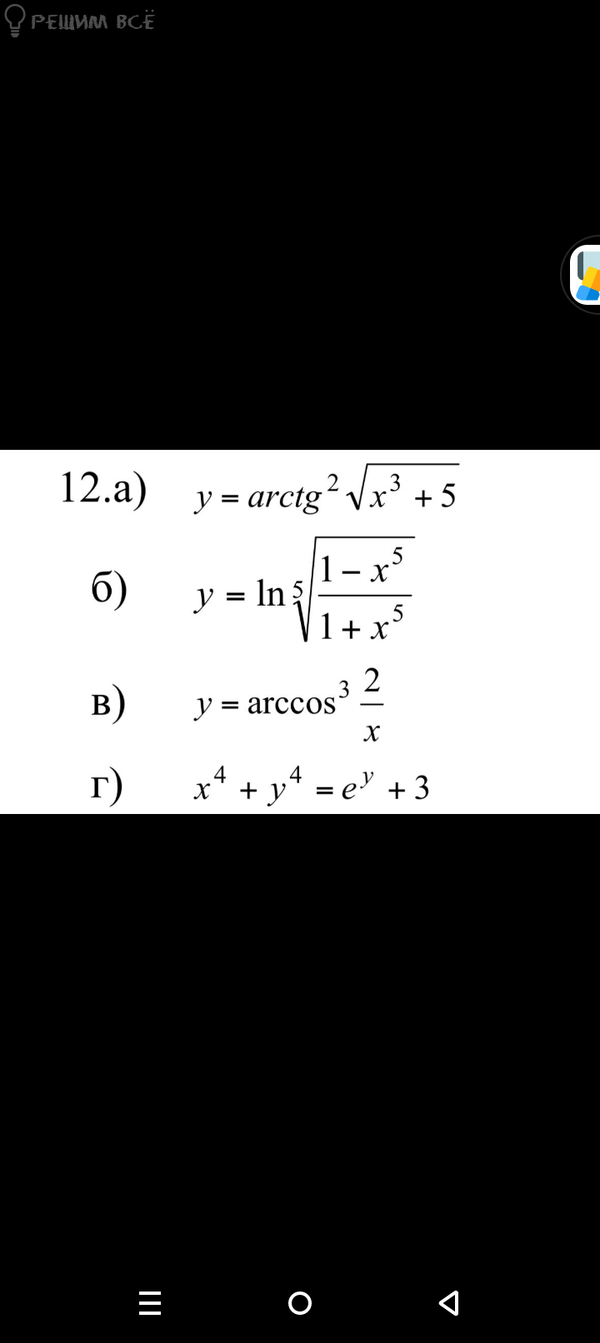
Решение
а) [m]y = arctg^2 \sqrt{x^3+5}[/m]
Производная от сложной функции равна произведению производных от каждой функции.
У нас здесь 4 функции, вложенных друг в друге.
y(f) = f^2 ; f(g) = arctg (g); g(h) = sqrt(h); h(x) = x^3 + 5
Берем производную от каждой функции:
[m]y'(f) = 2f(g) = 2 arctg(g) = 2 arctg \sqrt{x^3+5}[/m]
[m]f'(g) = \frac{1}{1+g^2} = \frac{1}{1+x^3+5} = \frac{1}{x^3 + 6}[/m]
[m]g'(h) = \frac{1}{2 \sqrt{h}} = \frac{1}{2 \sqrt{x^3+5}};\ \ h'(x) = 3x^2[/m]
И перемножаем это всё:
[m]y' = 2 arctg \sqrt{x^3+5} \cdot \frac{1}{x^3 + 6} \cdot \frac{1}{2 \sqrt{x^3+5}} \cdot 3x^2 = [/m]
[m]y' = \frac{arctg \sqrt{x^3+5} \cdot 3x^2}{(x^3 + 6) \sqrt{x^3+5}}[/m]
б) [m]y = \ln \sqrt[5]{\frac{1 - x^5}{1 + x^5}}[/m]
Здесь чуть полегче - 3 функции друг в друге.
[m]y(f) = \ln f;\ \ f(g) = \sqrt[5]{g} = g^{1/5};\ \ g(x) = \frac{1 - x^5}{1 + x^5}[/m]
Берем производную от каждой функции:
[m]y'(f) = \frac{1}{f(g)} = \sqrt[5]{\frac{1 + x^5}{1 - x^5}}[/m]
[m]f'(g) = \frac{1}{5} \cdot g^{-4/5} = \frac{1}{5} \cdot \sqrt[5]{(\frac{1 + x^5}{1 - x^5})^4}[/m]
[m]g'(x) = \frac{-5x^4(1+x^5) - 5x^4(1-x^5)}{(1+x^5)^2} = \frac{-5x^4 - 5x^9 - 5x^4+ 5x^9}{(1+x^5)^2} = \frac{-10x^4}{(1+x^5)^2}[/m]
И перемножаем это всё:
[m]y' = \sqrt[5]{\frac{1 + x^5}{1 - x^5}} \cdot \frac{1}{5} \cdot \sqrt[5]{(\frac{1 + x^5}{1 - x^5})^4} \cdot (-\frac{10x^4}{(1+x^5)^2}) =[/m]
[m] = -\frac{1}{5} \cdot \frac{1 + x^5}{1 - x^5} \cdot \frac{10x^4}{(1+x^5)^2} = -\frac{2x^4}{(1+x^5)(1 - x^5)} = -\frac{2x^4}{1 - x^{10}} = \frac{2x^4}{x^{10} - 1}[/m]