В равнобедренную трапецию можно вписать окружность. Найдите расстояние от точки пересечения диагоналей трапеции до её большего основания, если периметр трапеции равен 68, а площадь равна 255.
математика 8-9 класс
8173
В четырехугольник можно вписать окружность, если суммы противоположных сторон равны, т.е. AB+CD=BC+AD. AB+CD=34. AB=CD=17 (т.к. трапеция равнобедренная). S=1/2(BC+AD)BH => 17BH=255 => BH=15. AH=(AD–BC)/2. Из треугольника АВН по теореме Пифагора АН=√(289–225)=√64=8. (АD–BC)/2=8 => АD–BC=16, AD+BC=34. Сложим почленно эти два равенства, получим: 2AD=50 => AD=25 => BC=34–25=9. Треугольники NMC и KMA подобны по двум углам (∠NМС=∠АМK как вертикальные, ∠NMC=∠MAK, как внутренние накрест лежащие) => MC/AK=NM/MK => 4,5/12,5=(15–MK)/MK => 9MK=375–25MK => 34MK=375 => MK=375/34 = 11 1/34
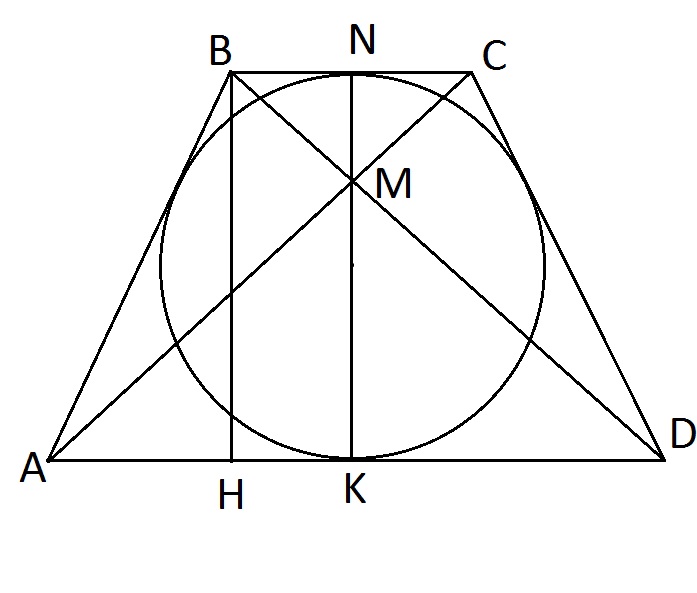
Ответ: 11 1/34
Обсуждения

