Задача 79178 Нужно ответ, без решения ...
Условие
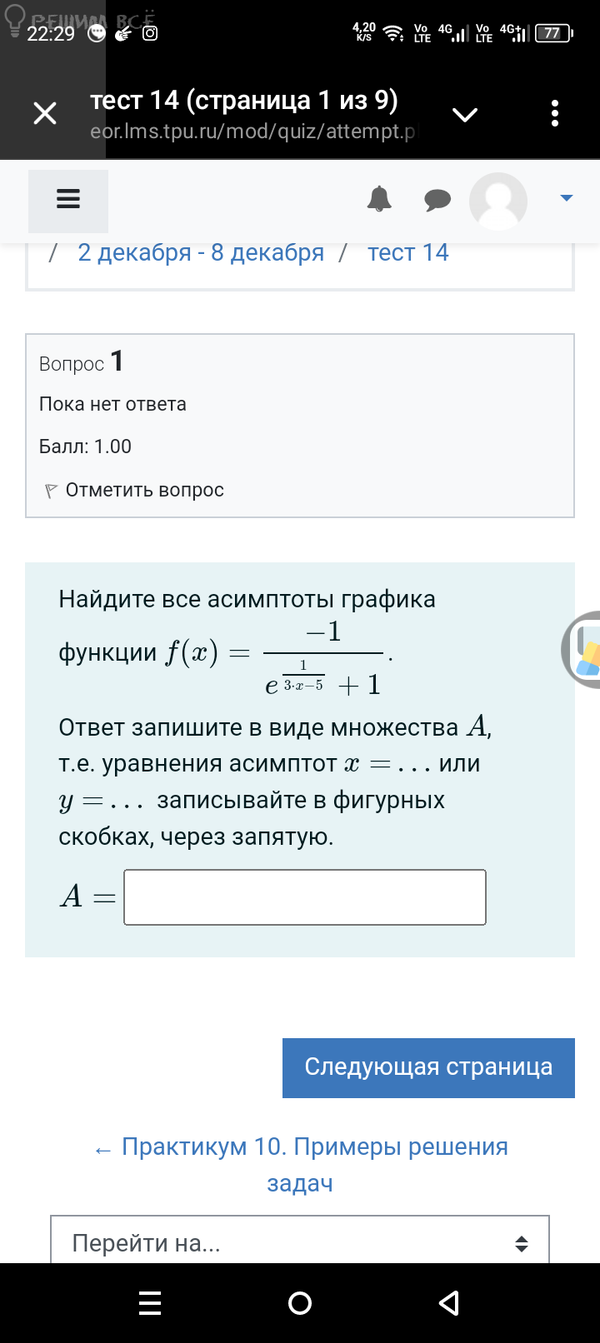
Решение
Будет неустранимый разрыв в точке:
3x - 5 = 0
x = 5/3 = 1,(6)
Найдем пределы слева и справа:
[m]\large \lim \limits_{x \to 5/3-0} -\frac{1}{e^{\frac{1}{3x-5}}+1} = -\frac{1}{e^{-\infty}+1} = -\frac{1}{0+1} = -1[/m]
[m]\large \lim \limits_{x \to 5/3+0} -\frac{1}{e^{\frac{1}{3x-5}}+1} = -\frac{1}{e^{+\infty}+1} = -\frac{1}{+\infty} = 0[/m]
Значит, при x = 5/3 нет асимптоты, а есть скачок функции.
На бесконечности будет асимптота f(x) = kx + b:
[m]\large k = \lim \limits_{x \to \infty} \frac{y(x)}{x} = \lim \limits_{x \to \infty} -\frac{1}{x(e^{\frac{1}{3x-5}}+1)} = -\frac{1}{\infty \cdot (e^{\frac{1}{\infty}}+1)} =[/m]
[m] = -\frac{1}{\infty \cdot (e^0+1)} = -\frac{1}{\infty \cdot 2} = 0[/m]
[m]\large b = \lim \limits_{x \to \infty} (y(x) - kx) = \lim \limits_{x \to \infty} -\frac{1}{e^{\frac{1}{3x-5}}+1} =[/m]
[m]= -\frac{1}{e^{\frac{1}{\infty}}+1} = -\frac{1}{e^0+1} = -\frac{1}{2} = -0,5[/m]
Ответ: Горизонтальная асимптота y = -0,5