Задача 7916 В окружности хорды АС и BD пересекаются...

larisashakirova

19.03.2016

В окружности хорды АС и BD пересекаются в точке M. Найдите BM, если AM = 2, СМ = 1,5, BD = 4 и BM < DM.

Произведения отрезки пересекающихся хорд равны: АМ•МС=ВМ•MD. BM=x, MD=4-x => 2•1,5=x(4-х) => x^2-4x+3=0
D=16-12=4
x1=(4-2)/2=1
x2=(4+2)/2=3
BM=1 => MD=3, BM<MD
BM=3 => MD=1, BM>MD, что противоречит условию. Ответ 1.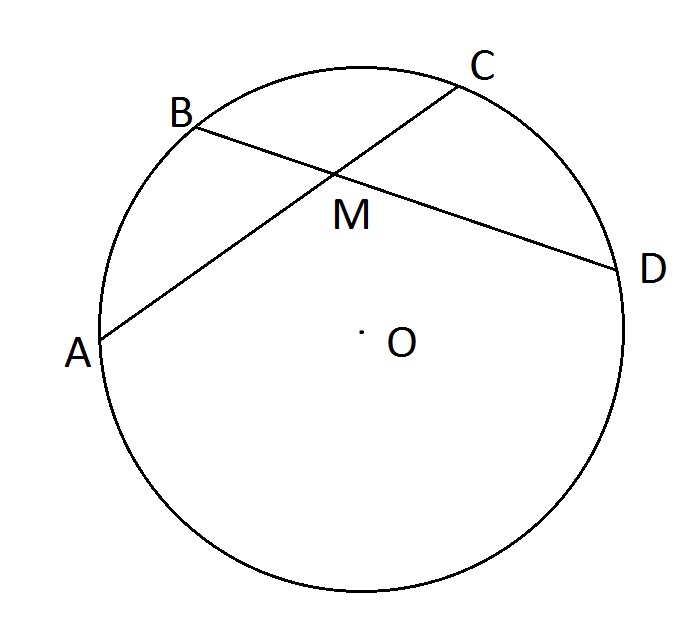

Ответ: 1