Постройте график функции y=(x-4)/(x^2-4x) - 1 и определите, при каких значениях к прямая у=к не имеет с графиком ни одной общей точки.
математика 8-9 класс
10600
Упростим функцию: y=(x-4)/x(x-4)-1 => y=1/x-1, x≠0, х≠4 - обратная пропорциональность, график расположен в 1 и 3 четвертях, сдвиг вниз на 1 единицу. Прямая y=k не имеет с графиком функции ни одной общей точки при k=-1 и -3/4.
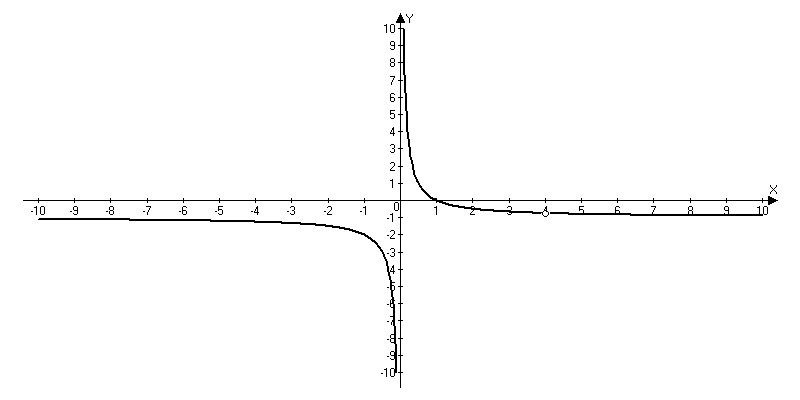
Ответ: -1, -3/4
Вопросы к решению (2)
у=–1 горизонтальная асимптота функции, поэтому прямая у=–1 не имеет с графиком ни одной общей точки. х≠4 => y≠1/4–1≠–3/4=> y=–3/4 не имеет с графиком общих точек.
у=-1 горизонтальная асимптота функции, поэтому прямая у=-1 не имеет с графиком ни одной общей точки. х≠4 => y≠1/4-1≠-3/4=> y=-3/4 не имеет с графиком общих точек.

