Задача 79083 Нужно только ответ, без решения ...
Условие
61
Решение
★
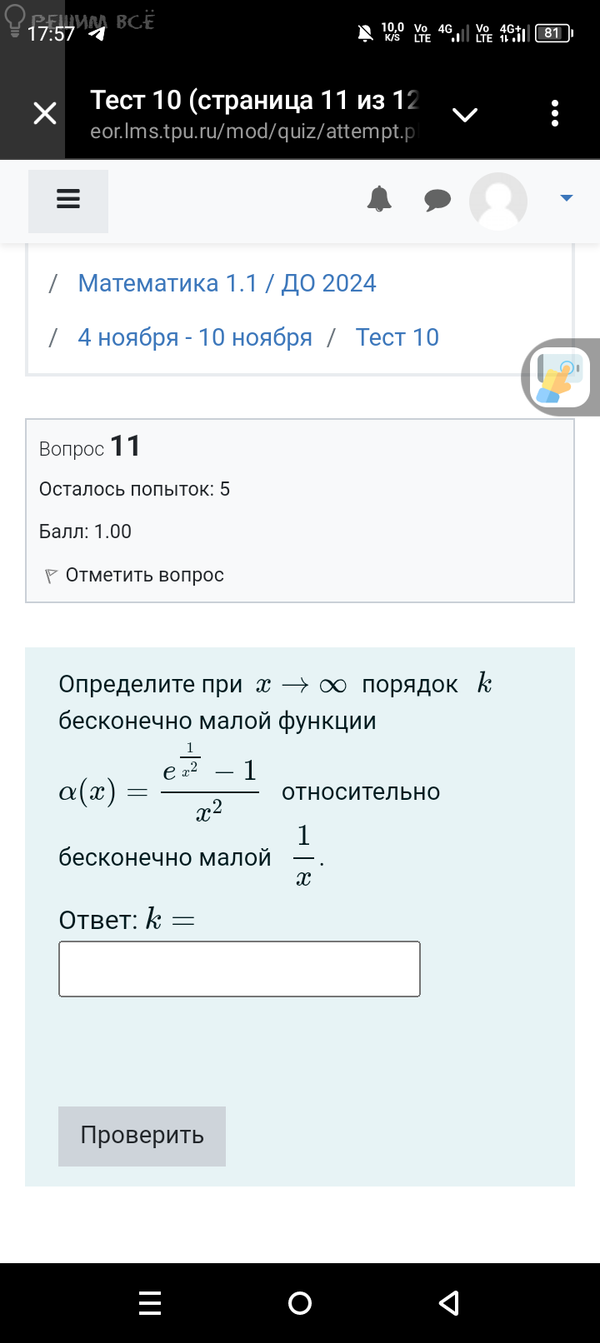
Согласно одному из следствий из 2 Замечательного предела:
[m]\lim \limits_{z \to 0} \frac{e^{z} - 1}{z} = 1[/m]
У нас z = 1/x^2 ⇒ 0
[m]\lim \limits_{1/x^2 \to 0} \frac{e^{1/x^2} - 1}{1/x^2 \cdot x^4} = \lim \limits_{1/x^2 \to 0} \frac{e^{1/x^2} - 1}{1/x^2} \cdot \lim \limits_{1/x^2 \to 0} \frac{1}{x^4} = 1 \cdot \lim \limits_{1/x \to 0} \frac{1}{x^4} = \lim \limits_{1/x \to 0} \frac{1}{x^4}[/m]
Так как x ⇒ oo, то 1/x ⇒ 0 имеет 1 порядок малости.
Очевидно, что 1/x^4 имеет 4 порядок малости.
[b]k = 4[/b]