Задача 79075 Нужно только ответ, без решения ...
Условие
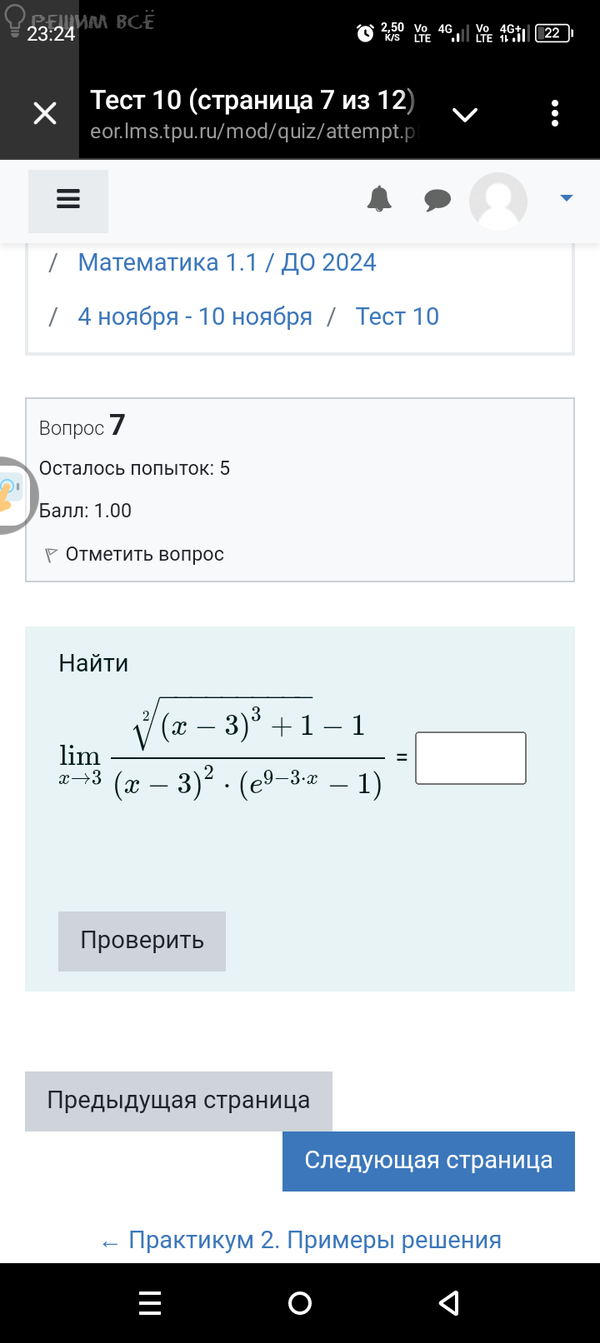
Решение
Она же не ставится на квадратных корнях.
[m] \large \lim \limits_{x \to 3} \frac{\sqrt{(x-3)^3 + 1} - 1}{(x-3)^2 \cdot (e^{9-3x} - 1)}[/m]
Домножаем числитель и знаменатель на скобку (sqrt((x-3)^3 + 1) + 1):
[m] \large \lim \limits_{x \to 3} \frac{(\sqrt{(x-3)^3 + 1} - 1)(\sqrt{(x-3)^3 + 1} + 1)}{(\sqrt{(x-3)^3 + 1} + 1)(x-3)^2 \cdot (e^{9-3x} - 1)} = \lim \limits_{x \to 3} \frac{(x-3)^3 + 1 - 1}{(\sqrt{(x-3)^3 + 1} + 1)(x-3)^2 \cdot (e^{9-3x} - 1)} =[/m]
[m]\large = \lim \limits_{x \to 3} \frac{(x-3)^3}{(\sqrt{(x-3)^3 + 1} + 1)(x-3)^2 \cdot (e^{9-3x} - 1)} = \lim \limits_{x \to 3} \frac{x-3}{(\sqrt{(x-3)^3 + 1} + 1) \cdot (e^{9-3x} - 1)}[/m]
Есть следствие из 2 Замечательного предела:
[m]\large \lim \limits_{z \to 0} \frac{e^{z} - 1}{z} = 1[/m]
В нашем случае z = 9 - 3x. Если x ⇒ 3, то 9 - 3x ⇒ 0. Переписываем так:
[m]\large \lim \limits_{x \to 3} \frac{x-3}{(\sqrt{(x-3)^3 + 1} + 1) \cdot (e^{9-3x} - 1)} = \lim \limits_{x \to 3} \frac{-3(x-3)}{-3(\sqrt{(x-3)^3 + 1} + 1) \cdot (e^{9-3x} - 1)} = [/m]
[m]\large = -\frac{1}{3} \cdot \lim \limits_{x \to 3} \frac{9-3x}{(\sqrt{(x-3)^3 + 1} + 1) \cdot (e^{9-3x} - 1)}=[/m]
[m]\large = -\frac{1}{3} \cdot \lim \limits_{x \to 3} \frac{1}{(\sqrt{(x-3)^3 + 1} + 1)} \cdot \lim \limits_{9 - 3x \to 0} \frac{9-3x}{(e^{9-3x} - 1)} =[/m]
[m]\large = -\frac{1}{3} \cdot \frac{1}{(\sqrt{(3-3)^3 + 1} + 1)} \cdot 1 = -\frac{1}{3} \cdot \frac{1}{(\sqrt{1} + 1)} = -\frac{1}{3 \cdot 2} = -\frac{1}{6}[/m]