Задача 79004 Найти производную сложной функции и...
Условие
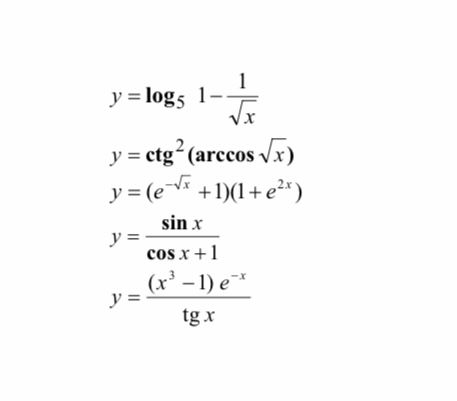

Решение
[m]y = f(g(x));\ \ y' = f'(g) \cdot g'(x)[/m]
В первом множителе мы берем производную от внешней функции f, считая всю внутреннюю функцию g, как переменную.
1) Если это действительно сложная функция, то скобки забыли.
[m]y = \log_5 (1 - \frac{1}{\sqrt{x}}) = \log_5 (1 - x^{-1/2})[/m]
Здесь [m]g(x) = 1 - x^{-1/2};\ \ f(g) = \log_5 (g)[/m]
[m]y' = \frac{1}{(1 - x^{-1/2}) \cdot \ln 5} \cdot (-\frac{1}{2} \cdot x^{-3/2}) = -\frac{1}{2 \ln 5} \cdot \frac{1}{(1 - x^{-1/2})} \cdot \frac{1}{\sqrt{x^3}}[/m]
2) y = ctg^2 (arccos sqrt(x))
Здесь аж 4 вложенных функции: y = f1(f2(f3(f4(x))))
[m]f4(x) = \sqrt{x};\ \ f4'(x) = \frac{1}{2\sqrt{x}}[/m]
[m]f3(f4) = arccos (f4);\ \ f3'(f4) = -\frac{1}{\sqrt{1 - f4^2}} = -\frac{1}{\sqrt{1 - x}}[/m]
[m]f2(f3) = ctg (f3);\ \ f2'(f3) = -\frac{1}{\sin^2 (f3)} = -\frac{1}{\sin^2 (arccos \sqrt{x})}[/m]
[m]f1(f2) = (f2)^2;\ \ f1'(f2) = 2f2 = 2ctg (arccos \sqrt{x})[/m]
Окончательно получаем:
[m]y' = f1'(f2) \cdot f2'(f3) \cdot f3'(f4) \cdot f4'(x)[/m]
[m]y' = 2ctg (arccos \sqrt{x}) \cdot (-\frac{1}{\sin^2 (arccos \sqrt{x})}) \cdot (-\frac{1}{\sqrt{1 - x}}) \cdot \frac{1}{2\sqrt{x}}[/m]
Минус на минус при умножении дает плюс, 2 сокращаются:
[m] \large y' = \frac{ctg (arccos \sqrt{x})}{\sin^2 (arccos \sqrt{x})} \cdot \frac{1}{\sqrt{1 - x}} \cdot \frac{1}{\sqrt{x}}[/m]
3) [m]y = (e^{-\sqrt{x}} + 1)(1 + e^{2x})[/m]
Здесь произведение двух сложных функций. y = f1(g1(x))*f2(g2(x)).
Производная от произведения берется так:
[m]y' = f1'(g1) \cdot g1'(x) \cdot f2(g2) + f1(g1) \cdot f2'(g2) \cdot g2'(x)[/m]
[m]g1(x) = -\sqrt{x};\ \ g1'(x) = -\frac{1}{2\sqrt{x}}[/m]
[m]f1(g1) = e^{g1} + 1 = e^{-\sqrt{x}} + 1;\ \ f1'(g1) = e^{g1} = e^{-\sqrt{x}}[/m]
[m]g2(x) = 2x;\ \ g2'(x) = 2[/m]
[m]f2(g2) = 1+e^{g2} = 1 + e^{2x};\ \ f2'(g2) = e^{g2} = e^{2x}[/m]
Окончательно получаем:
[m]y' = e^{-\sqrt{x}} \cdot (-\frac{1}{2\sqrt{x}}) \cdot (1 + e^{2x}) + (e^{-\sqrt{x}} + 1) \cdot e^{2x} \cdot 2[/m]
[m]y' = -\frac{e^{-\sqrt{x}}}{2\sqrt{x}} \cdot (1 + e^{2x}) + 2e^{2x}(e^{-\sqrt{x}} + 1)[/m]
4) [m]y = \frac{\sin x}{\cos x + 1}[/m]
Здесь дробь, y = f1(x)/f2(x). Производная от нее берется так:
[m]y' = \frac{f1'(x) \cdot f2(x) - f1(x) \cdot f2'(x)}{(f2(g))^2}[/m]
f1(x) = sin x; f1'(x) = cos x
f2(g) = cos x + 1; f2'(x) = -sin x
Окончательно получаем:
[m]y' = \frac{\cos x \cdot (\cos x + 1) - \sin x \cdot (-\sin x)}{(\cos x + 1)^2} = \frac{\cos^2 x + \cos x + \sin^2 x}{(\cos x + 1)^2} = \frac{1 + \cos x}{(\cos x + 1)^2} = \frac{1}{\cos x + 1} [/m]
5) [m]y = \frac{(x^3-1)e^{-x}}{tg\ x}[/m]
Здесь опять дробь, но в числителе произведение. y = f1(x)*f2(x)/f3(x)
Производная берется так:
[m]y' = \frac{f1'(x) \cdot f2(x) \cdot f3(x) + f1(x) \cdot f2'(x) \cdot f3(x) - f1(x) \cdot f2(x) \cdot f3'(x)}{(f3(x))^2}[/m]
f1(x) = x^3 - 1; f1'(x) = 3x^2
f2(x) = e^(-x); f2'(x) = -e^(-x)
f3(x) = tg x; f3'(x) = 1/cos^2 x
[m]y' = \large \frac{3x^2 \cdot e^{-x} \cdot tg\ x + x^3 \cdot (-e^{-x}) \cdot tg\ x - x^3 \cdot e^{-x} \cdot 1/\cos^2 x}{tg^2 x}[/m]
[m]y' = \large \frac{e^{-x} \cdot tg\ x \cdot x^2(3 - x) - x^3 \cdot e^{-x} \cdot 1/\cos^2 x}{tg^2 x}[/m]
[m]y' = \large \frac{\cos^2 x \cdot e^{-x} \cdot tg\ x \cdot x^2(3 - x) - x^3 \cdot e^{-x}}{tg^2 x \cdot \cos^2 x}[/m]
[m]y' = \large x^2 \cdot e^{-x} \cdot \frac{(\sin x \cos x (3 - x) - x)}{\sin^2 x} = \frac{x^2}{e^{x}} \cdot \frac{(\sin x \cos x (3 - x) - x)}{\sin^2 x}[/m]