Задача 78984 Нужно только ответ, без решения ...
Условие

Решение
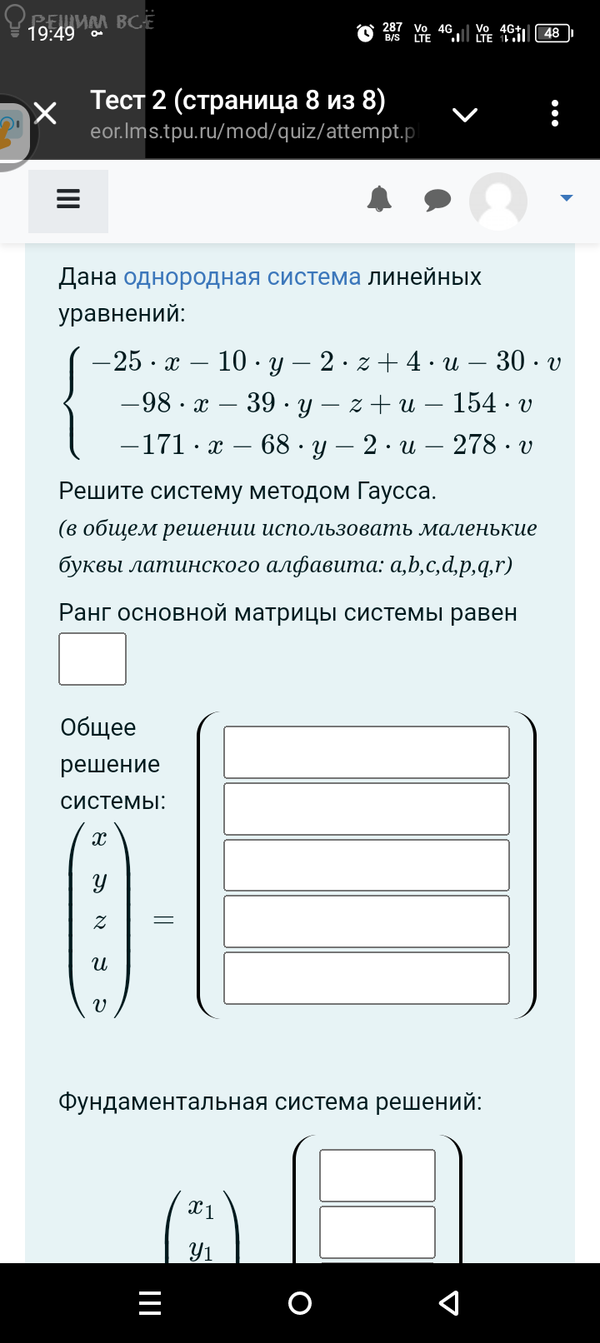
{ -98x - 39y - z + u - 154v = 0
{ -171x - 68y + 0z - 2u - 278v = 0
Поменяем знаки во всех уравнениях, от этого решение не меняется.
{ 25x + 10y + 2z - 4u + 30v = 0
{ 98x + 39y + z - u + 154v = 0
{ 171x + 68y + 0z + 2u + 278v = 0
Расширенная матрица системы:
[m]\begin{pmatrix}
25 & 10 & 2 & -4 & 30 & | & 0 \\
98 & 39 & 1 & -1 & 154 & | & 0 \\
171 & 68 & 0 & 2 & 278 & | & 0 \\
\end{pmatrix}[/m]
Умножаем 1 строку на 98, 2 строку на -25 и складываем их.
Умножаем 1 строку на 171, 3 строку на -25 и складываем их.
[m]\begin{pmatrix}
25 & 10 & 2 & -4 & 30 & | & 0 \\
0 & 5 & 171 & -367 & -910 & | & 0 \\
0 & 10 & 342 & -734 & -1820 & | & 0 \\
\end{pmatrix}[/m]
3 строку делим на 2:
[m]\begin{pmatrix}
25 & 10 & 2 & -4 & 30 & | & 0 \\
0 & 5 & 171 & -367 & -910 & | & 0 \\
0 & 5 & 171 & -367 & -910 & | & 0 \\
\end{pmatrix}[/m]
2 и 3 строки одинаковы, тожно 3 строку убрать:
[m]\begin{pmatrix}
25 & 10 & 2 & -4 & 30 & | & 0 \\
0 & 5 & 171 & -367 & -910 & | & 0 \\
\end{pmatrix}[/m]
Ранг расширенной матрицы равен 2.
Система compatible (совместна).
Запишем ее в виде системы с новыми коэффициентами:
{ 25x + 10y + 2z - 4u + 30v = 0
{ 0x + 5y + 171z - 367u - 910v = 0
Переменные z, u, v - базовые, они могут быть какими угодно.
z, u, v ∈ (-oo; + oo). Можно записать z, u, v ∈ R
y = (910v + 367u - 171z)/5
Подставляем в 1 уравнение:
25x + 10(910v + 367u - 171z)/5 + 2z - 4u + 30v = 0
25x + 1820v + 734u - 342z + 2z - 4u + 30v = 0
25x + 1850v + 730u - 340z = 0
25x = 340z - 730u - 1850v
x = (340z - 730u - 1850v)/25
x = (68z - 146u - 370v)/5
Ответ: Ранг расширенной матрицы равен 2.
Система compatible (совместна).
z, u, v ∈ (-oo; + oo)
y = (910v + 367u - 171z)/5
x = (68z - 146u - 370v)/5