Задача 78976 ...
Условие
Решение
Дан треугольник ABC, его стороны AB = BC = AC = 10sqrt(3) см.
Дана точка K, которая равноудалена от всех сторон треугольника:
|KM| = |KN| = |KP| = 13 см
Найти расстояние от К до плоскости треугольника.
Решение. Проверим, не лежит ли точка К в плоскости треугольника.
Тогда она должна совпадать с точкой О - центром вписанной окружности.
Формула радиуса окружности, вписанной в равносторонний треугольник:
[m]\large r = \frac{a \cdot \sqrt{3}}{6} = \frac{10 \sqrt{3} \cdot \sqrt{3}}{6} = \frac{10 \cdot 3}{6} = 5[/m] см
|OM| = |ON| = |OP| = r = 5 см
5 < 13, значит, точка K лежит вне плоскости и нам надо найти расстояние |KO|.
Но треугольники KOM, KON, KOP - прямоугольные. По теореме Пифагора:
[m]|KO|^2 = |KM|^2 - |OM|^2 = 13^2 - 5^2 = 169 - 25 = 144[/m]
[m]|KO| = \sqrt{144} = 12[/m] см
Ответ: 12 см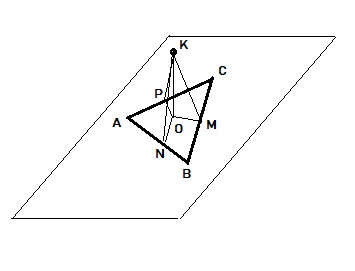
Все решения
r = a√3 / 6 (Формула радиуса вписанной окружности правильного треугольника)
r = (10√3 см)√3 / 6 = 5 см (Подстановка и вычисление радиуса)
d = h - r (где d - искомое расстояние, h - расстояние от точки K до плоскости, проходящей через центр вписанной окружности)
h = 13 см (Дано: расстояние от точки K до каждой стороны)
d = 13 см - 5 см = 8 см (Подстановка и вычисление искомого расстояния)