Задача 78949 Надо решить задачу 4 и 2б...
Условие

Решение
1) Область определения: D(Y): x > 0
2) Вертикальная асимптота - при x = 0,
[m]\lim \limits_{x \to 0+0} (x^2 - 2 \ln x) = 0 - (-\infty) = +\infty[/m]
Других точек разрыва нет и вертикальных асимптот больше нет.
3) Пересечение с осями.
x = 0 - не входит в область определения.
Пересечения с осью Oy нет.
x^2 - 2*ln x = 0
x^2 = 2*ln x
Алгебраически это уравнение непонятно, как решать.
Но оно легко решается графически.
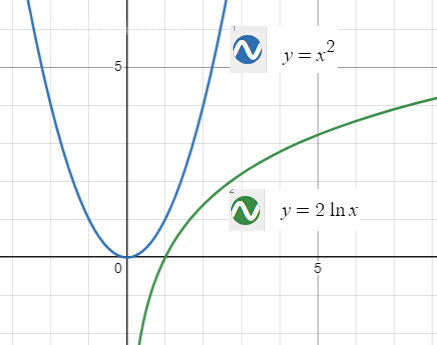
Смотри рисунок 1.
Графики y1 = x^2 и y2 = 2*ln x не пересекаются.
Значит, решений нет.
Пересечения с осью Ox нет.
4) Четность: не четная и не нечетная, функция общего вида.
5) Периодичность: не периодическая.
6) Критические точки 1 порядка: y' = 0
y' = 2x - 2/x = 0
2x = 2/x
x - 1/x = 0
(x^2 - 1)/x = 0
(x - 1)(x + 1)/x = 0
x1 = -1 - не подходит по области определения.
x2 = 1, y(1) = 1^2 - 2*ln 1 = 1
Знаки производной слева и справа от критической точки:
y'(0,5) = 2*0,5 - 2/0,5 = 1 - 2*2 = 1 - 4 = -3 < 0
При x ∈ (0; 1) функция убывает.
y'(2) = 2*2 - 2/2 = 4 - 1 = 3 > 0
При x ∈ (1; +oo) функция возрастает.
Значит, критическая точка M(1; 1) это точка минимума.
7) Критические точки 2 порядка. y'' = 0
y'' = 2 - (-2/x^2) = 2 + 2/x^2 > 0 при любом x > 0
Значит, точек перегиба нет, функция всюду выпуклая вниз (вогнутая).
8) Горизонтальные и наклонные асимптоты.
[b]f(x) = kx + b[/b]
[m]k = \lim \limits_{x \to +\infty} \frac{y(x)}{x} = \lim \limits_{x \to +\infty} \frac{x^2 - 2\ln x}{x}= \lim \limits_{x \to +\infty} (x - \frac{2\ln x}{x}) = +\infty - \frac{2\ln \infty}{\infty} = +\infty[/m]
Горизонтальных и наклонных асимптот нет.
9) Область значений функции. E(Y): y ∈ [1; +oo)
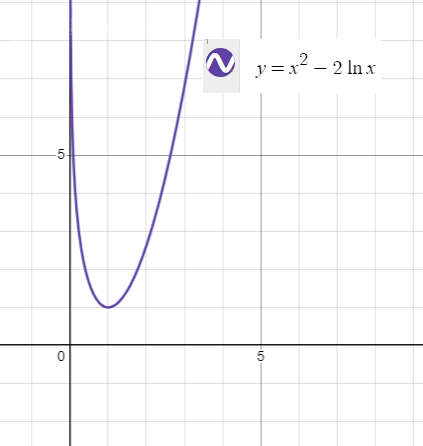
10) График смотрите на рисунке 2.