Задача 78944 ...

Lundawn

11 декабря 2024 г. в 09:30

Проверить, что для любых множеств A, B, C выполнение включения A ∪ B ⊆ C влечет выполнение включения A ∪ B ⊆ B ∪ C

626fab9a354ab65fb2f43abb

11 декабря 2024 г. в 11:17

★

Легче всего это проверить по диаграмма Эйлера – Венна.
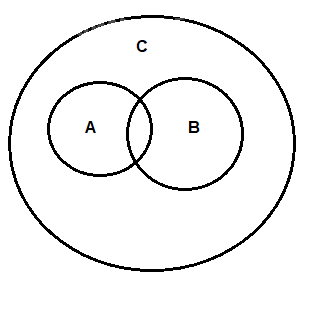
Смотрите рисунок.
Есть три круга – A, B, C.
Круг С расположен так, что объединение кругов A и B находится внутри C.
Это и означает, что: A U B ⊆ C
Но тогда объединение B U C = C, потому что круг B внутри круга С.
И вместо отношения:
A U B ⊆ B U C
Получаем отношение:
A U B ⊆ C
Которое, как мы знаем, изначально верное по условию.
Доказано.