Задача 78844 Дано уравнение линии 2у^2+8х+12у-3=0 ....

Эльмира_367496172

29 ноября 2024 г. в 06:36

Дано уравнение линии 2у²+8х+12у–3=0 . Построить линию, записав это уравнение в нормальной форме. Записать координаты фокусов. Если эта линия окажется параболой, то записать уравнение директрисы.

Удачник66

29 ноября 2024 г. в 09:37

★

2y² + 8x + 12y – 3 = 0
2y² + 12y – 3 + 8x = 0
2(y² + 6y + 9 – 9) + 8x – 3 = 0
2(y + 3)² – 18 – 3 + 8x = 0
2(y + 3)² = –8x + 21
2(y + 3)² = –8(x – 21/8)
Обе части уравнения можно разделить на 2:
(y + 3)² = –4(x – 21/8)
(y + 3)² = –4(x – 2,625)
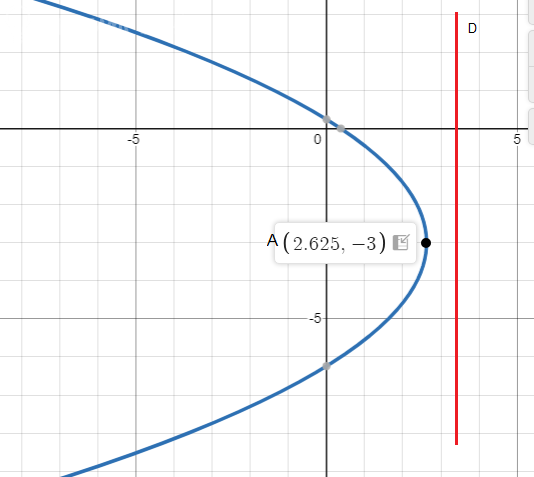
Это парабола, ее вершина A(x0; y0) = A(2,625; –3)

Каноническое уравнение параболы:
(y – y0)² = 2p·(x – x0)
Параметр:
2p = –4
p = –2
Уравнение директрисы:
x = –p/2 + x0
x = 1 + 21/8
x = 29/8 = 3 5/8 = 3,625

Чертеж прилагается, директриса D нарисована красным.