Задача 78838 Номер 3 не надо решить, а остальное по...
Условие

Решение
p = 3a + 2b;
|p|^2 = |3a|^2 + |2b|^2 - 2*|3a|*|2b|*cos(π - (a, b))
|p|^2 = 6^2 + 2^2 - 2*6*2*cos π/3 = 36 + 4 - 24*1/2 = 28
|p| = sqrt(28) = 2sqrt(7)
q = a - b
|q|^2 = |a|^2 + |b|^2 - 2*|a|*|b|*cos (a, b)
|q|^2 = 2^2 + 1^2 - 2*2*1*cos 2π/3 = 4 + 1 - 4*(-1/2) = 7
|q| = sqrt(7)
Скалярное произведение векторов p и q:
p*q = (3a + 2b)*(a - b) = 3a^2 + 2ab - 3ab - 2b^2 = 3a^2 - ab - 2b^2
p*q = 3|a|^2 - |a|*|b|*cos(a, b) - 2*|b|^2 = 3*2^2 - 2*1*cos (2π/3) - 2*1^2 =
p*q = 3*4 - 2*(-1/2) - 2*1 = 12 + 1 - 2 = 11
Угол между векторами p и q:
[m]\cos \phi = \frac{p \cdot q}{|p| \cdot |q|} = \frac{11}{2\sqrt{7} \cdot \sqrt{7}} = \frac{11}{14}[/m]
[m]\phi = arccos\ \frac{11}{14}[/m]
2) N(2; -3; sqrt(7))
Точка M на оси абсцисс имеет координаты (x; 0; 0).
|MN| = sqrt((x - 2)^2 + (0 + 3)^2 + (0 - sqrt(7))^2) = 5
(x - 2)^2 + 3^2 + 7 = 25
(x - 2)^2 = 25 - 7 - 9 = 9
x - 2 = -3; [b]x1 = -1[/b]
x - 2 = 3; [b]x2 = 5[/b]
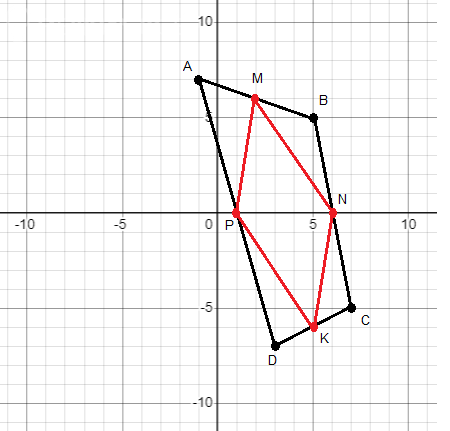
3) A(-1; 7); B(5; 5); C(7; -5); D(3; -7)
Доказать, что 4-угольник, образованный серединами сторон 4-угольника ABCD, является параллелограммом.
На рисунке Вершины 4-угольника отмечены черным.
Найдем середины сторон: M = (AB)/2, N = (BC)/2, K = (CD), P = (DA)/2
M = ((-1+5)/2; (7+5)/2) = (4/2; 12/2) = (2; 6)
N = ((5+7)/2; (5-5)/2) = (12/2; 0/2) = (6; 0)
K = ((7+3)/2; (-5-7)/2) = (10/2; -12/2) = (5; -6)
P = ((3-1)/2; (-7+7)/2) = (2/2; 0/2) = (1; 0)
На рисунке середины сторон 4-угольника отмечены красным.
Чтобы проверить, что MNKP - параллелограмм, построим уравнения сторон.
[m](MN):\ \frac{x - 6}{2 - 6} = \frac{y - 0}{6-0}[/m]
[m](MN):\ \frac{x - 6}{-4} = \frac{y}{6}[/m]
[m](KP):\ \frac{x - 5}{1-5} = \frac{y+6}{0+6}[/m]
[m](KP):\ \frac{x - 5}{-4} = \frac{y+6}{6}[/m]
У прямых (MN) и (KP) коэффициенты (знаменатели) одинаковые, значит, они параллельны друг другу.
[m](NK):\ \frac{x - 6}{5 - 6} = \frac{y - 0}{-6-0}[/m]
[m](NK):\ \frac{x - 6}{-1} = \frac{y}{-6}[/m]
[m](PM):\ \frac{x - 2}{1-2} = \frac{y-6}{0-6}[/m]
[m](PM):\ \frac{x - 2}{-1} = \frac{y-6}{-6}[/m]
У прямых (NK) и (PM) коэффициенты (знаменатели) одинаковые, значит, они параллельны друг другу.
Так как противоположные стороны попарно параллельны, то MNKP - параллелограмм.
[b]Теорема доказана.[/b]
4) с = {0; 2; -3}; d = {-3; 2; -1}
Найти координаты вектора b || c, если скалярное произведение b*d = 6
Так как вектора b || c, то координаты b пропорциональны координатам c.
Обозначим координаты вектора b = {0; 2k; -3k}, где k - коэф. пропорциональности.
Скалярное произведение векторов через координаты:
x(b)*x(d) + y(b)*y(d) + z(b)*z(d) = b*d
0*(-3) + 2k*2 + (-3k)*(-1) = 6
4k + 3k = 6
7k = 6
k = 6/7
[b]b = {0; 12/7; -18/7}[/b]
5) A(2; -1); B(1; 2); |AP| = 3sqrt(10)
Найти координаты точки P.
Уравнение прямой AB по двум точкам:
[m](AB):\ \frac{x - 2}{1 - 2} = \frac{y + 1}{2 + 1}[/m]
[m](AB):\ \frac{x - 2}{-1} = \frac{y + 1}{3}[/m]
3(x - 2) = -1(y + 1)
3x - 6 + y + 1 = 0
3x + y - 5 = 0
y = 5 - 3x
Точка P находится на расстоянии 3sqrt(10) от точки A и лежит на луче BA.
Значит, координаты точки P можно записать как P(x; 5 - 3x)
|AP| = sqrt((x - 2)^2 + (5 - 3x + 1)^2) = 3sqrt(10)
|AP|^2 = (x - 2)^2 + (6 - 3x)^2 = 9*10
x^2 - 4x + 4 + 36 - 36x + 9x^2 = 90
10x^2 - 40x + 40 - 90 = 0
x^2 - 4x - 5 = 0
(x - 5)(x + 1) = 0
x1 = -1; y1 = 5 - 3*(-1) = 8; P(-1; 8) - не лежит на луче BA.
x2 = 5; y2 = 5 - 3*5 = -10; [b]P(5; -10)[/b] - это ответ.
6) Полярную систему координат я не помню, изучал 40 лет назад.