Задача 78801 привести уравнения кривых второго...

67445ba4b5964965cc2d059f

11/26/2024 6:52:32 AM

привести уравнения кривых второго порядка к каноническому виду, построить кривые, найти координаты фокусов

626fab9a354ab65fb2f43abb

11/26/2024 9:52:01 AM

★

x^2 + 4y^2 + 4x - 24y + 36 = 0
Соберем отдельно x, отдельно y:
(x^2 + 4x) + (4y^2 - 24y) + 36 = 0
Выделяем полные квадраты:
(x^2 + 4x + 4 - 4) + 4(y^2 - 6y + 9 - 9) + 36 = 0
Получаем квадраты суммы или разности:
(x + 2)^2 - 4 + 4(y - 3)^2 - 36 + 36 = 0
Приводим подобные и переносим числа направо:
(x + 2)^2 + 4(y - 3)^2 = 4
Делим всё уравнение на 4:
(x + 2)^2/4 + (y - 3)^2/1 = 1
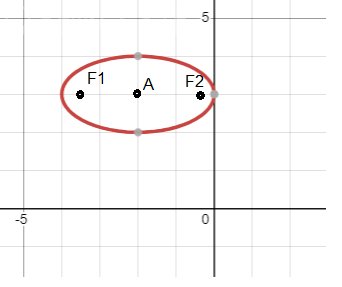
Это уравнение эллипса с центром A(x0; y0) = A(-2; 3) и полуосями:
a = sqrt(4) = 2, b = 1, c = sqrt(a^2 - b^2) = sqrt(4 - 1) = sqrt(3)
Координаты фокусов:
F1(x0 - c; y0) = F1(-2 - sqrt(3); 3)
F2(x0 + c; y0) = F1(-2 + sqrt(3); 3)
Эксцентриситет:
ε = c/a = sqrt(3)/2