Задача 78744 Напишите уравнение окружности,...

673849115a00e67c51d41b00

11/16/2024 7:28:46 AM

Напишите уравнение окружности, проходящей через точки А(1;5) и В(7;-1), если её центр лежит на прямой у = x - 2

626fab9a354ab65fb2f43abb

11/16/2024 9:02:15 AM

★

По сути требуется найти такую точку C(x, y) на прямой y = x - 2, которая находится на одинаковом расстоянии радиуса от точек A(1; 5) и B(7; -1).
Так как точка C находится на этой прямой, то ее координаты можно записать так: C(x; x-2)
Расстояния между точками находим так:
|AC| = sqrt((x-1)^2 + (y-5)^2) = sqrt((x-1)^2 + (x-2-5)^2) = sqrt((x-1)^2 + (x-7)^2)
|BC| = sqrt((x-7)^2 + (y+1)^2) = sqrt((x-7)^2 + (x-2+1)^2) = sqrt((x-7)^2 + (x-1)^2)
Приравниваем эти расстояния:
sqrt((x-1)^2 + (x-7)^2) = sqrt((x-7)^2 + (x-1)^2)
Слева и справа выражения одинаковые.
Значит, любая точка на прямой y = x - 2 может быть центром окружности.
Возьмем, например, точку C(1; -1), тогда:
R = |AC| = sqrt((x-1)^2 + (y-5)^2) = sqrt((1-1)^2 + (-1-5)^2) = sqrt(0^2 + (-6)^2) = sqrt(36) = 6
Уравнение окружности:
[b](x - 1)^2 + (y + 1)^2 = 36[/b]
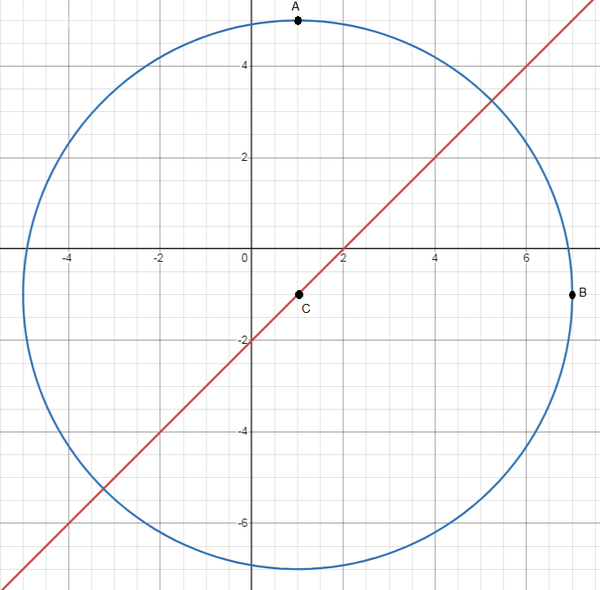
Смотрите рисунок