Задача 78737 Надо решить эту задачу...
Условие

математика ВУЗ
154
Решение
★
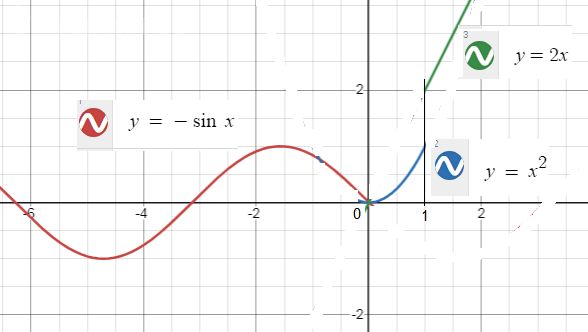
Значит, разрывы могут быть только на стыке функций, в точках x1 = 0, x2 = 1.
Проверяем значения функции слева и справа от этих точек.
1) y(x1 - 0) = y(0 - 0) = -sin 0 = 0 - значение слева в точке x1
y(x1 + 0) = y(0 + 0) = 0^2 = 0 - значение справа в точке x1
Значения равны, значит, в точке x1 = 0 разрыва нет.
2) y(x2 - 0) = y(1 - 0) = 1^2 = 1 - значение слева в точке x2
y(x2 + 0) = y(1 + 0) = 2*1 = 2 - значение справа в точке x2
Значения разные, значит, в точке x2 = 1 есть разрыв.
Это неустранимый разрыв 1 рода - скачок.
Чертеж смотрите на рисунке.