Задача 78715 Для следующих кривых второго порядка: 1)...
Условие
1) Определите тип;
2) Сделайте это каноническим;
3) найти все характеристики (директриса, фокус, эксцентриситет, асимптоты и т. д.)k.);
4) нарисуйте форму.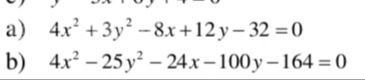
Решение
a) 4x^2 + 3y^2 - 8x + 12y - 32 = 0
4x^2 - 8x + 4 - 4 + 3y^2 + 12y + 12 - 12 - 32 = 0
Выделяем полные квадраты:
4(x^2 - 2x + 1) - 4 + 3(y^2 + 4y + 4) - 12 - 32 = 0
4(x - 1)^2 + 3(y + 2)^2 = 48
Делим всё уравнение на 48:
(x - 1)^2/12 + (y + 2)^2/16 = 1
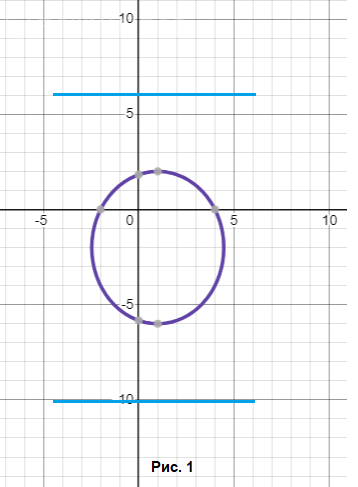
Это эллипс с центром A(1; -2),
Полуоси a = sqrt(12); b = 4,
Так как a < b, то:
c = sqrt(b^2 - a^2) = sqrt(16 - 12) = sqrt(4) = 2
Эксцентриситет: ε = c/b = 2/4 = 0,5
Фокусы: F1(x0; y0 - с) = F1(1; -4); F2(x0; y0 + с) = F2(1; 0)
Директрисы: y1 = y0 - b/ε; y2 = y0 + b/ε
y1 = -2 - 4/0,5 = -2 - 8 = -10; y2 = -2 + 4/0,5 = -2 + 8 = 6
Смотрите Рис. 1. Директрисы показаны голубым цветом.
b) 4x^2 - 25y^2 - 24x - 100y - 164 = 0
4x^2 - 24x + 36 - 36 - 25y^2 - 100y - 100 + 100 - 164 = 0
Выделяем полные квадраты:
4(x^2 - 6x + 9) - 36 - 25(y^2 + 4y + 4) + 100 - 164 = 0
4(x - 3)^2 - 25(y + 2)^2 = 100
Делим всё уравнение на 100:
(x - 3)^2/25 - (y + 2)^2/4 = 1
Это гипербола с центром A(3; -2)
Полуоси a = 5; b = 2
Так как a > b, то:
c = sqrt(b^2 + a^2) = sqrt(4 + 25) = sqrt(29)
Эксцентриситет: ε = c/a = sqrt(29)/5
Фокусы: F1(x0 - с; y0) = F1(3 - sqrt(29); -2); F2(x0 + с; y0) = F2(3 + sqrt(29); -2)
Директрисы: x1 = x0 - a/ε; x2 = x0 + a/ε
x1 = 3 - 5 : (sqrt(29)/5) = 3 - 25/sqrt(29) = (87 - 25sqrt(29))/29 ≈ -1,64;
x2 = 3 + 5 : (sqrt(29)/5) = 3 + 25/sqrt(29) = (87 + 25sqrt(29))/29 ≈ 7,64
Асимптоты: y1 = y0 - b/a*x; y2 = y0 + b/a*x
y1 = -2 - 2/5*(x - x0) = -0,4*(x - 3) - 2 = -0,4*x - 0,8;
y2 = -2 + 2/5*( - x0)x = 0,4*(x - 3) - 2 = 0,4*x - 3,2
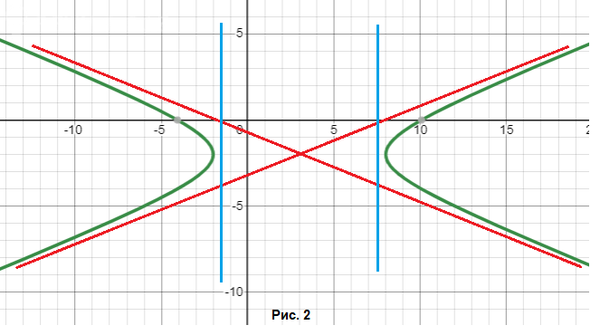
Смотрите Рис. 2. Директрисы показаны голубым цветом.
Асимптоты показаны красным цветом.