Задача 78712 Исследовать функцию ...
Условие

Решение
2) Функция общего вида, так как f(x) ≠ f(-x):
f(-x) = (-x)^(3) - 6(-x)^(2) + 9(-x) - 3 = -(x)^(3) - 6x^(2) - 9x - 3
3) Найдем пересечение с Оу:
х = 0, у = 0 - 6*0 + 9*0 - 3 = -3 => пересечение с осью у в точке (0;-3)
4) Возьмем производную и определим точки минимума и максимума функции:
y' = 3x^(2) - 12x + 9
3x^(2) - 12x + 9 = 0 | :3
x^(2) - 4x + 3 = 0 => х1 = 3, х2 = 1 по теореме Виета.
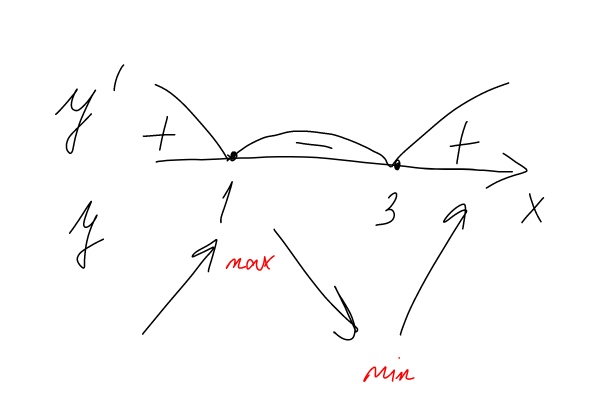
Точки минимума и максимума иксов видны на рис. 1 (х max = 1, x min = 3). Найдем минимум и максимум по игреку, подставив значения:
у max(1) = 1 - 6 + 9 - 3 = 1
y min(3) = 3^(3) - 6*3^(2) + 9*3 - 3 = 27 - 54 + 27 - 3 = -3
Функция возрастает на промежутке: (- ∝ ; 1] ∪ [3;+ ∝ )
Убывает при х ∈ [1;3].
5) Найдем точку перегиба. Для этого возьмем вторую производную:
y' = 3*x^(2) - 12x + 9 = 6x - 12
6x - 12 = 0
6x = 12 => x = 2
Эта точка и будет являться точкой перегиба по Х (рис.2). Для У: 2^(3) - 6*2^(2) + 9*2 - 3 = 8 - 24 + 18 - 3 = -1
6) По полученным данным можем построить график функции (рис.3)
7) Е(у) = (-∝; +∝)