Задача 78642 ...
Условие
Найдите вероятности событий:
1) X>0;
2) X≤2;
3) X=4.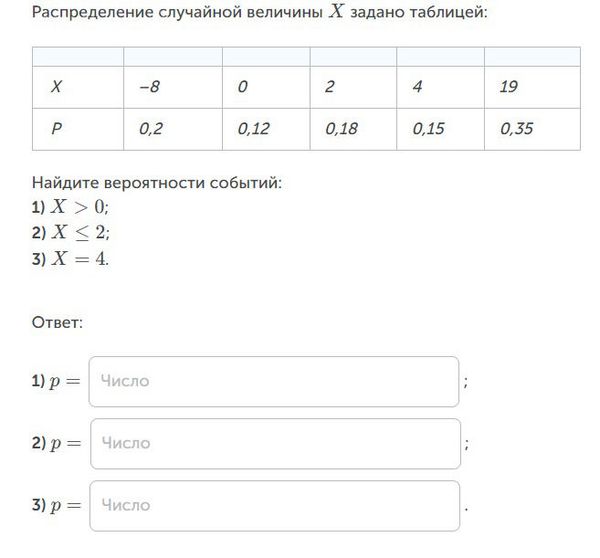
Решение
Распределение случайной величины [m] X [/m] задано таблицей:
[m]
\begin{array}{|c|c|c|c|c|c|}
\hline
X & -8 & 0 & 2 & 4 & 19 \\
\hline
P & 0.2 & 0.12 & 0.18 & 0.15 & 0.35 \\
\hline
\end{array}
[/m]
Найдём вероятности событий:
1) [m] X > 0 [/m]
2) [m] X \leq 2 [/m]
3) [m] X = 4 [/m]
Решение:
1) Вероятность того, что [m] X > 0 [/m] равна сумме вероятностей случаев, когда [m] X [/m] принимает значения 2, 4 и 19.
[m]
P(X > 0) = P(X = 2) + P(X = 4) + P(X = 19) = 0.18 + 0.15 + 0.35 = 0.68
[/m]
2) Вероятность того, что [m] X \leq 2 [/m] равна сумме вероятностей случаев, когда [m] X [/m] принимает значения -8, 0 и 2.
[m]
P(X \leq 2) = P(X = -8) + P(X = 0) + P(X = 2) = 0.2 + 0.12 + 0.18 = 0.5
[/m]
3) Вероятность того, что [m] X = 4 [/m] равна вероятности соответствующего события.
[m]
P(X = 4) = 0.15
[/m]
Ответ:
1) [m] p = 0.68 [/m];
2) [m] p = 0.5 [/m];
3) [m] p = 0.15 [/m].