Задача 7862 Окружность радиуса R касается...

Julia_Trusova

17.03.2016

Окружность радиуса R касается продолжений сторон ВС и АС треугольника ВС А и стороны ВА. Найдите периметр треугольника ВСА, если R=sqrt(З), а угол ВСА = 60°.

CM и CN - касательные к вневписанной окружности, значит CM=CN.
По теореме : Расстояние от вершины треугольника до точки касания вневписанной окружности с продолжением боковой стороны равно его полупериметру.
Значит, CN=р.
СО - биссектриса ∠ BCA, ⇒ ∠OCN=30°.
△OCN-прямоугольный(ON-радиус вневписанной окружности, проведенный в точку касания, ⇒ ON⊥NC)
ON=sqrt(3). так как ∠OCN=30°, ON=1/2*OC, ⇒ OC=2*sqrt(3)
По теореме Пифагора:
NC=sqrt((2*sqrt(3))^2-(sqrt(3))^2)=sqrt(12-3)=3.
Значит, р=3, тогда Р=3*2=6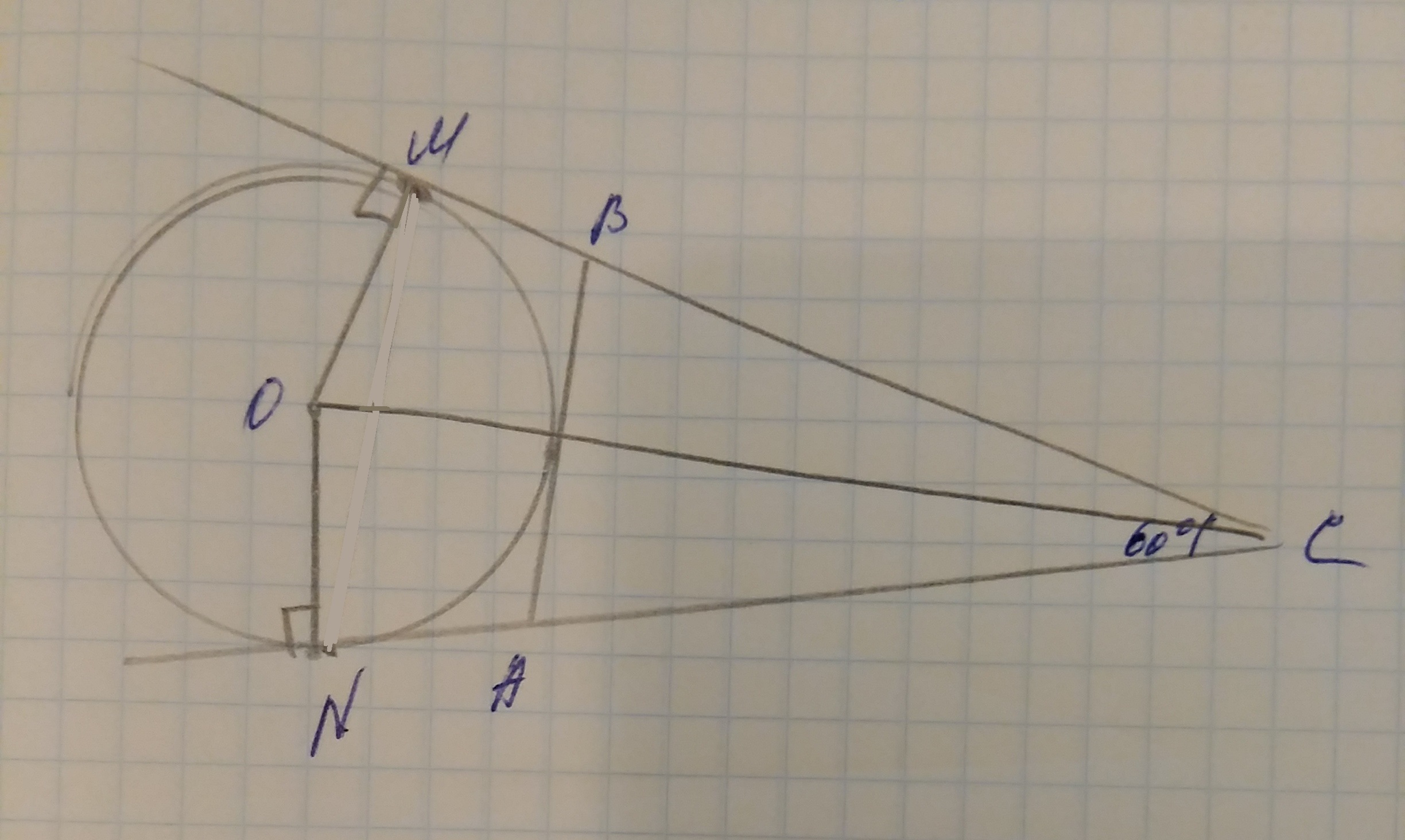

Ответ: 6