Задача 78614 ...
Условие
вести уравнение кривой второго порялка к каноническому виду.
Определить тип кривой. Найти се полуоси, эксцентриситет, ко-
ординаты вершин и фокусов, уравнения директрис и асимптот
(если они имеются), Сделать чертеж.
2x² - 4x- y² - 4y - 6 =0
Решение
2(x^2 - 2x) - (y^2 + 4y) - 6 = 0
Дополняем скобки до полного квадрата и вычитаем таки же числа:
2(x^2 - 2x + 1 - 1) - (y^2 + 4y + 4 - 4) - 6 = 0
Сворачиваем квадраты суммы или разности:
2(x - 1)^2 - 2 - (y + 2)^2 + 4 - 6 = 0
2(x - 1)^2 - (y + 2)^2 = 4
Делим всё на 4:
(x - 1)^2/2 - (y + 2)^2/4 = 1
Это каноническое уравнение гиперболы.
Её центр (1; -2), полуоси a = sqrt(2); b = 2, c = sqrt(a^2+b^2) = sqrt(2+4) = sqrt(6)
Эксцентриситет ε = c/a = sqrt(6)/sqrt(2) = sqrt(3)
Фокусы: F1(1 - sqrt(6); -2); F2(1 + sqrt(6); -2)
Уравнения директрис: x1 = x0 - a/ε; x2 = x0 + a/ε
x1 = 1 - sqrt(2)/sqrt(3) = 1 - sqrt(6)/3 ≈ 0,2; x2 = 1 + sqrt(6)/3 ≈ 1,8
Уравнения асимптот: y1 = -b/a*x; y2 = b/a*x
y1 = -2/sqrt(2)*x + y0 = -sqrt(2)*x - 2; y2 = sqrt(2)*x - 2
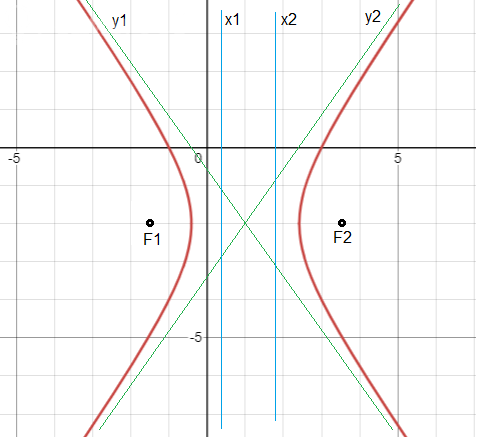
Чертеж прилагается.
Асимптоты показаны зеленым цветом, директрисы синим цветом.