Задача 78609 Исследуйте функцию двух переменных на...
Условие
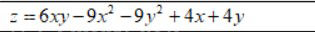
Решение
1. **Исходная функция:**
z = 6xy - 9x^2 - 9y^2 + 4x + 4y
2. **Частные производные:**
∂z/∂x = 6y - 18x + 4
∂z/∂y = 6x - 18y + 4
3. **Система уравнений:**
1) 6y - 18x + 4 = 0
2) 6x - 18y + 4 = 0
4. **Решение первого уравнения для y:**
6y = 18x - 4
y = 3x - 2/3
5. **Подстановка y во второе уравнение:**
6x - 18(3x - 2/3) + 4 = 0
6x - 54x + 12 + 4 = 0
-48x + 16 = 0
48x = 16
x = 1/3
6. **Подставляем x обратно для нахождения y:**
y = 3(1/3) - 2/3
y = 1 - 2/3
y = 1/3
7. **Критическая точка:**
(x, y) = (1/3, 1/3)
8. **Значение функции в критической точке:**
z = 6(1/3)(1/3) - 9(1/3)^2 - 9(1/3)^2 + 4(1/3) + 4(1/3)
z = 6(1/9) - 9(1/9) - 9(1/9) + 4/3 + 4/3
z = 2/3 - 1 - 1 + 8/3
z = (2 + 8 - 6)/3
z = 4/3
9. **Проверка типа экстремума:**
Вычисляем вторые производные:
∂²z/∂x² = -18
∂²z/∂y² = -18
∂²z/∂x∂y = 6
Формируем матрицу Гессе:
H = | -18 6 |
| 6 -18 |
10. **Определитель матрицы Гессе:**
D = (-18)(-18) - (6)(6)
D = 324 - 36
D = 288 (D > 0)
11. **Вывод:**
Поскольку D > 0 и ∂²z/∂x² < 0, то в критической точке (1/3, 1/3) находится максимум.
**Ответ:**
Критическая точка: (1/3, 1/3)
Значение функции: z = 4/3
Это максимум.