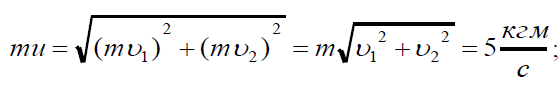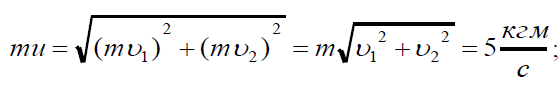По гладкой горизонтальной плоскости движутся по взаимно перпендикулярным направлениям две частицы, имеющие одинаковые массы m =1 кг. Скорость первой частицы v1=3 м/c ,второй v2=4 м/c. В результате столкновения первая частица останавливается. Определите импульс p второй частицы после столкновения.
физика 10-11 класс
5469
Так как после столкновения скорость первой частицы равна нулю, то, согласно закону сохранения импульса, импульс второй частицы будет равен сумме импульсов первой и второй частиц до столкновения. mv1+mv2=mu. Так как v1 перпендикулярно v2, то
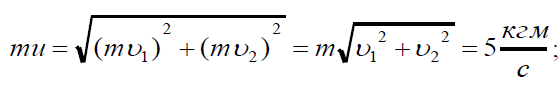
Ответ: 5 кгм/c