Задача 78558 Задана функция y=f(x). Найти точки...
Условие
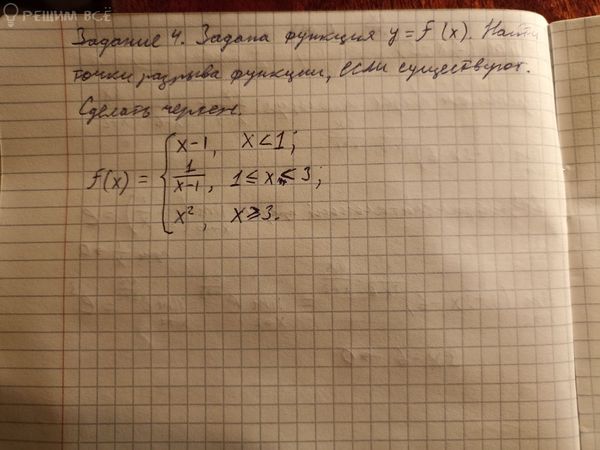
математика ВУЗ
394
Решение
★
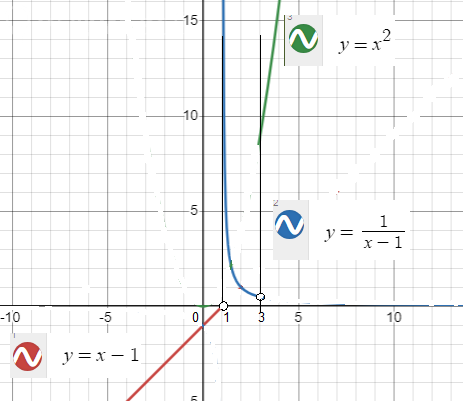
2 функция: f(x) = 1/(x - 1); 1 ≤ x < 3
3 функция: f(x) = x^2; x ≥ 3
1 функция непрерывна.
2 функция имеет в точке x = 1 неустранимый разрыв 2 рода - бесконечность.
3 функция непрерывна.
Проверим точку перехода x = 3:
[m]\lim \limits_{x \to 3-0} f(x) = \lim \limits_{x \to 3-0} \frac{1}{x-1} = \frac{1}{3-1} = \frac{1}{2}[/m]
[m]\lim \limits_{x \to 3+0} f(x) = \lim \limits_{x \to 3+0} x^2 = 3^2 = 9[/m]
В точке x = 3 неустранимый разпыв 1 рода - скачок.
График смотрите на рисунке.