Задача 78531 Решить систему линейных однородных...
Условие
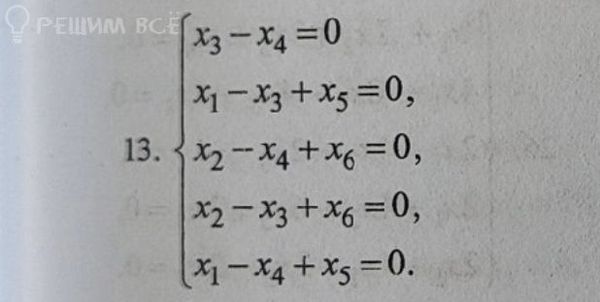
Решение
{ x1 - x3 + x5 = 0
{ x2 - x4 + x6 = 0
{ x2 - x3 + x6 = 0
{ x1 - x4 + x5 = 0
Как и всякая однородная система, она имеет решение (0; 0; 0; 0; 0; 0).
Уравнений 5, а переменных 6, поэтому система неопределенная.
То есть она имеет кроме этого ещё бесконечно много решений.
Из 1 уравнения:
[b]x4 = x3[/b]
Подставляем в остальные уравнения:
{ x4 = x3
{ x1 - x3 + x5 = 0
{ x2 - x3 + x6 = 0
{ x2 - x3 + x6 = 0
{ x1 - x3 + x5 = 0
Как видим, 2 уравнение совпадает с 5, а 3 уравнение совпадает с 4.
Запишем сокращённую систему:
{ x4 = x3
{ x1 - x3 + x5 = 0
{ x2 - x3 + x6 = 0
Выразим x5 и x6 через остальные переменные:
{ x4 = x3
{ x5 = -x1 + x3
{ x6 = -x2 + x3
Получили:
x1; x2; x3 - базисные переменные, любые действительные числа.
x4; x5; x6 - свободные переменные, зависят от базисных по формулам.
Можно записать так:
x1; x2; x3 ∈ R; x4 = x3; x5 = -x1 + x3; x6 = -x2 + x3
Ответ: (x1; x2; x3; x3; -x1+x3; -x2+x3); x1; x2; x3 ∈ R