Задача 78519 Решите относительно условия ...
Условие
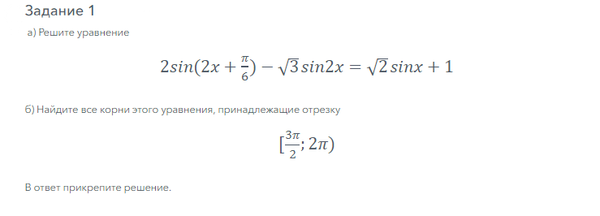
Решение
Найти корни на промежутке [3π/2; 2π]
2(sin 2x cos π/6 + cos 2x sin π/6) - sqrt(3)sin 2x = sqrt(2)sin x + 1
2sin 2x*sqrt(3)/2 + 2cos 2x*1/2 - sqrt(3)sin 2x = sqrt(2)sin x + 1
sin 2x*sqrt(3) + cos 2x - sqrt(3)sin 2x = sqrt(2)sin x + 1
sqrt(3)sin 2x сокращается:
cos 2x = sqrt(2)sin x + 1
1 - 2sin^2 x = sqrt(2)sin x + 1
1 сокращается, 2sin^2 x переносим направо:
0 = 2sin^2 x + sqrt(2)sin x
sqrt(2)sin x*(sqrt(2)sin x + 1) = 0
Если произведение равно 0, то один из множителей равен 0.
1) sin x = 0;
[b]x1 = π*k[/b]
2) sqrt(2)sin x + 1 = 0
sin x = -1/sqrt(2)
[b]x2 = (-1)^n*(-π/4) + π*n[/b]
Общее решение уравнения:
[b]x1 = π*k; x2 = (-1)^n*(-π/4) + π*n[/b]
Решения на промежутке [3π/2; 2π]:
x1 = 2π - π/4
[b]x1 = 7π/4; x2 = 2π[/b]