Задача 785 Однородный стержень массы m закреплен в...
Условие
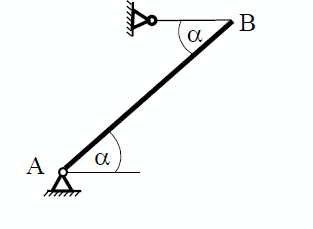
физика 10-11 класс
7011
Решение

Ответ: T=mg/2


Ответ: T=mg/2