Задача 7848 Площадь основания конуса равна 63....

echan2018

16 марта 2016 г.

Площадь основания конуса равна 63. Плоскость, параллельная плоскости основания конуса, делит его высоту на отрезки длиной 1 и 2, считая от вершины. Найдите площадь сечения конуса этой плоскостью.

Сечением является круг. Необходимо найти площадь этого круга.
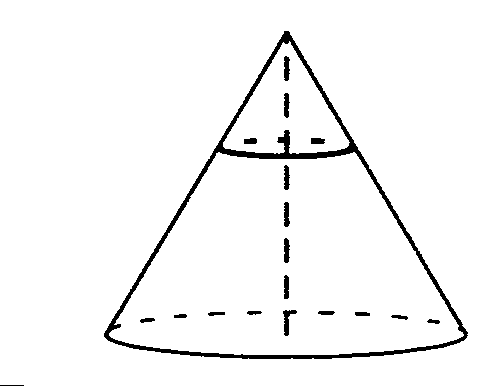
Обозначим вершину конуса за A, а центр основания за B, а центр сечения за O
Решаем через подобие: площади подобных фигур относятся друг к другу, как коэффициент подобия в квадрате.
AO/OB=1/2 ⇒ AB=1+2=3
AB/AO=3/1 – коэффициент подобия
S=(3/1)²·x
63=9/1·x
x=63/9
x=7



Ответ: 7