Задача 78472 ,""J"‘/—\I;x;«u:o_ 1-y? ...
Условие
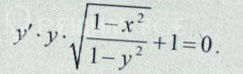
Решение
[m]y' \cdot y \cdot \sqrt{ \frac{1-x^2}{1-y^2} } + \sqrt{ \frac{1-y^2}{1-y^2} } = 0[/m]
[m]\frac{y' \cdot y \cdot \sqrt{1-x^2}}{\sqrt{1-y^2}} + \frac{\sqrt{1-y^2}}{\sqrt{1-y^2}} = 0[/m]
Умножаем всё на [m]\sqrt{1-y^2}[/m]
[m]y' \cdot y \cdot \sqrt{1-x^2} + \sqrt{1-y^2} = 0[/m]
Уравнение с разделяющимися переменными:
[m]-y \cdot \sqrt{1-x^2} \frac{dy}{dx} = \sqrt{1-y^2}[/m]
[m]-\frac{y\ dy}{\sqrt{1-y^2}} = \frac{dx}{\sqrt{1-x^2}}[/m]
Правый интеграл простой:
[m]\int \frac{dx}{\sqrt{1-x^2}} = arcsin(x) + C[/m]
Левый чуть сложнее:
[m]\int (-\frac{y\ dy}{\sqrt{1-y^2}})[/m]
Замена 1 - y^2 = t; dt = -2y dy; -y dy = 1/2 dt
[m]\int \frac{dt}{2\sqrt{t}} = \sqrt{t} = \sqrt{1 - y^2}[/m]
Получили уравнение:
[m]\sqrt{1 - y^2} = arcsin(x) + C[/m]
Можно оставить в таком неявном виде, а можно довести до явного:
[m]1 - y^2 = (arcsin(x) + C)^2[/m]
[m]y^2 = 1 - (arcsin(x) + C)^2[/m]
[m]y = ± \sqrt{1 - (arcsin(x) + C)^2}[/m]
Но это нежелательно, знак ± в функции не приветствуется.
Лучше оставить в неявном виде.