Задача 78465 решите умоляюс решением...

Dennis_537695206

16 октября 2024 г. в 04:05

решите умоляюс решением

Удачник66

17 октября 2024 г. в 08:10

★

1) c) CB – CA – MK + BD – KD = CB + AC + KM + BD + DK =
= AC + CB + BD + DK + KM = AM
d) (AB + BC – DC) + (DK – MK) = AB + BC + CD + DK + KM = AM
Вектор –XY = YX, вектор просто меняет направление.
При суммировании вектора, как и числа,
можно менять местами, от этого сумма не меняется.

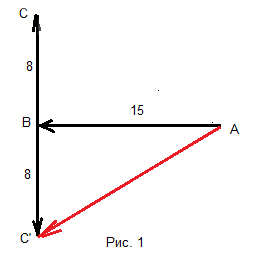
2) AB = 15; BC = 8; ∠ B = 90°
Смотрите рисунок 1.
|AB – BC| = |AB + BC'| = |AC'| = √|AB|² + |BC'|² = √15² + 8² =
= √225 + 64 = √289 = 17
Это гипотенуза прямоугольного треугольника, находим по т. Пифагора.
|AB| – |BC| = 15 – 8 = 7
Здесь просто вычитаются длины векторов, угол не имеет значения.

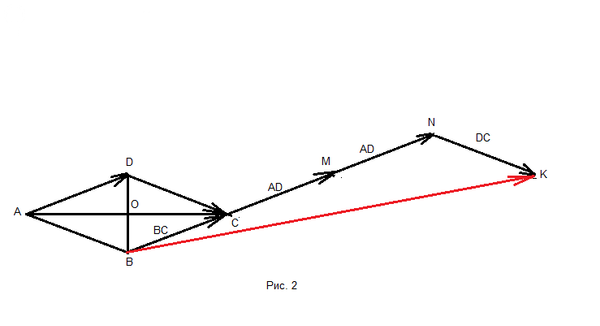
3) Ромб ABCD, диагонали |AC| = 24; |BD| = 10
Смотрите рисунок 2.
|BC – DA + AD – CD| = |BC + AD + AD + DC| = |BC + CM + MN + NK| = |BK|
Вектора BC = CM = MN = AD, NK = DC
∠ BNK = ∠ ADC, найдем его косинус.
|AO| = |AC|/2 = 24/2 = 12
|OD| = |BD|/2 = 10/2 = 5
|AD| = √|AO|² + |OD|² = √12² + 5² = √144 + 25 = √169 = 13
cos ADO = |OD|/|AD| = 5/13
∠ ADC = 2·∠ ADO
Косинус двойного угла:
cos ADC = 2·cos² ADO – 1 = 2·25/169 – 1 = 50/169 – 1 = –119/169
∠ BNK = ∠ ADC
У ромба все стороны одинаковые, поэтому стороны треугольника BNK:
|BN| = 3·|BC| = 3·13 = 39
|NK| = |BC| = 13
По теореме косинусов:
|BK|² = |BN|² + |NK|² – 2·|BN|·|NK|·cos BNK
|BK|² = 39² + 13² – 2·39·13·(–119/169) = 1521 + 169 + 2·3·13·13·119/169 =
= 1690 + 6·119 = 1690 + 714 = 1404
|BK| = √1404 ≈ 37,47